Процентное соотношение двух чисел формула excel

Подсчет процентов в табличном редакторе

Табличный редактор хорош тем, что большую часть вычислений он производит самостоятельно, а пользователю необходимо ввести только исходные значения и указать принцип расчета. Вычисление производится так: Часть/Целое = Процент. Подробная инструкция выглядит так:

1. Жмем на необходимую ячейку правой клавишей мышки.
2. В возникшем маленьком специальном контекстном меню необходимо выбрать кнопку, имеющую наименование «Формат ячеек».

Разберем небольшой пример, чтобы понять, как работать с процентной информацией в табличном редакторе. Подробная инструкция выглядит так:

У нас есть три колонки в табличке. В первой отображено наименование продукта, во второй – запланированные показатели, а в третьей – фактические.

Используя вышеприведенную инструкцию, переводим поле D2 в процентный вид.

Используя специальный маркер заполнения, растягиваем введенную формулу на всю колонку.

Готово! Табличный редактор сам высчитал процент реализации плана для каждого товара.

Способы расчета

В учебнике математики за 5-ый класс можно узнать, что % составляет сотую часть от числа. Чтобы узнать, сколько % от определенного значения, можно воспользоваться пропорцией и составить правило креста.

Например, нужно найти 500 от 1000. При этом данные, которые располагаются напротив друг друга необходимо перемножить, а затем разделить на третье число.

При этом числа пишутся под цифрами, а проценты под такими же показателями.Получается:

Можно использовать и программу Excel.

Сначала создайте на рабочем столе лист Excel.

Затем откройте документ и в выделенной строке введите:

• = (равно);
• затем 8500;
• после этого нажмите * (умножить);
• затем 15;
• после следует нажать клавишу % и Enter.

Способы расчета

В учебнике математики за 5-ый класс можно узнать, что % составляет сотую часть от числа. Чтобы узнать, сколько % от определенного значения, можно воспользоваться пропорцией и составить правило креста.

Например, нужно найти 500 от 1000. При этом данные, которые располагаются напротив друг друга необходимо перемножить, а затем разделить на третье число.

При этом числа пишутся под цифрами, а проценты под такими же показателями.Получается:

Можно использовать и программу Excel.

Сначала создайте на рабочем столе лист Excel.

Затем откройте документ и в выделенной строке введите:

• = (равно);
• затем 8500;
• после этого нажмите * (умножить);
• затем 15;
• после следует нажать клавишу % и Enter.

Практические навыки

ТР. показывает, сколько процентов составляет одно число от другого. С помощью ТП можно вычислить, на сколько процентов возросло или сократилось число относительно другого.

Использование формул

ТР не бывает отрицательным, а ТП может. ТП определяется на базе ТР, обратный порядок недопустим. Чтобы высчитать величину, применяется ПП, поскольку он наглядно отражает динамику изменений.

Можно на примере посчитать темп роста в процентах. Работник завода получал заработную плату каждый месяц в зависимости от выработки. В январе сотрудник получил 40000 рублей, в феврале 45000 р. ТР составляет по формуле: 45000/40000*100 = 112,5. Таким образом, в феврале доход относительно предыдущего месяца может исчисляться как 112%.

Формулы широко применяются в повседневной жизни населения. В интернете имеется онлайн-калькулятор, позволяющий получить реальный результат или проверить собственные решения. Их использование позволяет опустить ошибки расчетов.

Разные методы расчета

Наглядное использование формул на примере позволит проанализировать предназначение ТР и ТП. В таблице представлен внутренний валовой продукт России с 2010—2017 годы. Необходимо найти ТР (в процентах) базисным и цепным методами.

Таблица данных о ВВП в национальной валюте за 2011−2018 гг.

Период	ВВП России ТР	(%)
в млрд р.	Цепной метод	Базисный метод
2011	48 000	–	–
2012	57 698	120,2	120,2
2013	66 817	115,8	139,2
2014	71 117	106,4	148,2
2015	78 945	111,0	164,5
2016	80 826	102,4	168,4
2017	83 871	103,8	174,7
2018	88 177	105,1	183,7

Формула цепного метода: ТР= Yi / Yi -1*100.

Для 2011 величины не будет. Начиная с 2012 года: 57698/48000*100 = 120,2%. Для 2013 года: 66817/57698*100 = 115,8%. Таким способом высчитываются суммы для каждого периода.

Базисный метод: ТР = Yi/Ybasic*100. Это отношение к основному, первому коэффициенту. Например, для 2012 года суммы высчитываются 57698/48000*100 = 120,2%, для 2013 года: 66817/48000*100 = 115,8%. Таким принципом вычисляются все оставшиеся периоды.

Таким же способом рассчитывается процентное соотношение данных актива баланса, отчета о прибылях и убытках. Показатели, отражающие величину чистой прибыли за 2 года, позволят выявить прирост или снижение показателей.

Данные	2017	2018	ТР %
Выручка от реализации	1500000	1600000	106,7
Финансовые доходы	400000	350000	87,5

За 2018 год ТР составит 106,7% выручки, а доходы от вложений возросли на 87,5%.

ТР необходим, чтобы узнать, сколько процентов составляет одно значение от другого. Последним выступает предыдущее число. Темп прироста позволяет выяснить, насколько изменился заданный параметр.

На основе одного из коэффициентов нельзя составить верную оценку определяемому явлению (по международному, отечественному рынку, предприятию, показателю работоспособности фирмы). Необходимы комплексные меры изучения и расчетов показателей в динамике. Для анализа финансовой деятельности можно брать разную информацию из форм отчетности.

Расчет процентов по кредиту в Excel

Задача:
В кредит взяли 200 000 рублей на год. Процентная ставка – 19%. Погашать будем в течение всего срока равными платежами. Вопрос: какой размер ежемесячного платежа при данных условиях кредитования?

Важные условия для выбора функции: постоянство процентной ставки и сумм ежемесячных платежей. Подходящий вариант функция – «ПЛТ()». Она находиться в разделе «Формулы»-«Финансовые»-«ПЛТ»

1. Ставка – процентная ставка по кредиту, разделенная на количество периодов начисления процентов (19%/12, или В2/12).
2. Кпер – число периодов выплат по кредиту (12).
3. ПС – сумма займа (200 000 р., или В1).
4. Поля аргументов «БС» и «Тип» оставим без внимания.

Результат со знаком «-», т.к. деньги кредитополучатель будет отдавать.

Один процент — это сотая часть от числа. Данное понятие используется, когда нужно обозначить отношение доли к целому. Кроме этого, в процентах можно сравнивать несколько величин, при этом обязательно указывая, относительного какого целого проценты вычисляются. Например, расходы выше доходов на 10 % или цена на железнодорожные билеты возросла на 15 % в сравнении с тарифами прошлого года. Число процентов выше 100 означает, что доля превышает целое, как часто бывает при статистических расчетах.

Процент как финансовое понятие — плата, заемщика кредитору за предоставление денег во временное пользование. В бизнесе встречается выражение «работать за проценты». В данном случае подразумевается, что размер вознаграждения зависит от прибыли или оборота (комиссионные). Обойтись без вычисления процентов невозможно в бухгалтерии, бизнесе, банковском деле. Чтобы упростить расчеты, разработан онлайн-калькулятор процентов.

Калькулятор позволяет вычислить:

• Процент от заданного значения.
• Процент из суммы (налог по фактической зарплате).
• Процент от разницы (НДС из ).
• И многое другое…

При решении задач на калькуляторе процентов нужно оперировать тремя значениями, одно из которых неизвестно (по заданным параметрам вычисляется переменная). Сценарий расчета следует выбирать, исходя из заданных условий.

Свойство отношения

Отношение не изменится если его члены умножить или разделить на одно и тоже число.

Это одно из важнейших свойств отношения следует из свойства частного. Мы знаем, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. А поскольку отношение является ничем иным как делением, то свойство частного работает и для него.

Вернемся к отношению девочек к мальчикам (10: 5)
. Данное отношение показало, что на каждого мальчика приходится две девочки. Проверим, как работает свойство отношения, а именно попробуем умножить или разделить его члены на одно и то же число.

В нашем примере удобнее разделить члены отношения на их наибольший общий делитель (НОД).

НОД членов 10 и 5 это число 5. Поэтому можно разделить члены отношения на число 5

Получили новое отношение . Это есть отношение два к одному (2:1). Данное отношение, как и прошлое отношение 10:5
показывает, что на одного мальчика приходятся две девочки.

На рисунке показано отношение 2: 1
(два к одному). Как и в прошлом отношении 10: 5
на одного мальчика приходятся две девочки. Другими словами, отношение не изменилось.

Пример 2
. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз в первом классе девочек больше мальчиков? Во сколько раз во втором классе девочек больше мальчиков?

В обоих классах девочек в два раза больше мальчиков, поскольку отношения и равны одному и тому же числу.

Свойство отношения позволяет строить различные модели, которые имеют схожие параметры с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 метров и высоту 10 метров.

Чтобы нарисовать на бумаге похожий дом, нужно рисовать его в таком же отношении 30: 10
.

Разделим оба члена этого отношения на число 10. Тогда получим отношение 3: 1
. Это отношение равно 3, как и предыдущее отношение равно 3

Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров

3 м = 300 см

1 м = 100 см

Имеем отношение 300 см: 100 см. Разделим члены этого отношения на 100. Получим отношение 3 см: 1 см. Теперь можно нарисовать дом с шириной 3 см и высотой 1 см

Конечно нарисованный дом намного меньше реального дома, но неизменным осталось отношение ширины и высоты. Это позволило нам нарисовать дом, максимально похожий на реальный

Отношение можно понимать и другим образом. Изначально было сказано, что у реального дома ширина составляет 30 метров, а высота 10 метров. Итого получается 30+10, то есть 40 метров.

Эти 40 метров можно понимать, как 40 частей. Отношение 30: 10 говорит о том, что 30 частей приходится на ширину, а 10 частей на высоту.

Далее члены отношения 30: 10 были разделены на 10. В результате получилось отношение 3: 1. Это отношение можно понимать, как 4 части, три из которых приходится на ширину, одна — на высоту. В этом случае обычно требуется узнать сколько конкретно метров приходится на ширину и высоту.

Другими словами, нужно узнать сколько метров приходится на 3 части и сколько метров приходится на 1 часть. Сначала надо узнать сколько метров приходится на одну часть. Для этого общие 40 метров нужно разделить на 4, поскольку в отношении 3: 1 всего четыре части

Определим сколько метров приходится на ширину:

10 м × 3 = 30 м

Определим сколько метров приходится на высоту:

10 м × 1 = 10 м

Как найти базовую сумму исходя из ее процента

В некоторых случаях нам может быть известно какое-либо число и процент, которое оно составляет от базового числа. Нам необходимо определить значение. Например, нам может быть дана сумма 67, которое составляет 23% от базового числа. Каково же само базовое число?

Для решения этой задачи нам необходимо 67 разделить на 23 и умножить на 100. Формула вычисления процента выглядит следующим образом:

67 / B * 100 = A

Подставляем значения:

67 / 23 * 100 = 293, 31 (десятые после запятой можем округлить)

Проверяем полученный результат с помощью формулы из первого способа:

293, 31 / 100 * 23 = 67

Всё сошлось.

Как посчитать разницу между процентами в MS Excel

Нужное нам соотношение можно высчитать и с помощью редактора MS Excel. Обычно она высчитывается по уже описанной нами формуле:

Где:

• А2 – старый показатель
• B2 – новый показатель

Предположим, нам необходимо высчитать процентную разницу в результатах компании, которая в 2019 году продала товаров на 400 тысяч рублей, а во втором – на 730 тысяч рублей.

В Экселе это будет выглядеть следующим образом:

1. Внесите в ячейку А2 старый параметр, а в B2 – новый;

2. Установите курсор на ячейку С2 и выберите для неё процентный формат, кликнув на соответствующую кнопку во вкладке «Главная»;

3. Далее в ячейке С2 впишите формулу  =(B2-A2)/A2   и нажмите на ввод;

4. В ячейке С2 автоматически отобразится нужный результат;

5. При необходимости дополните значения ячеек А и B новыми параметрами ниже, и расширьте курсор ячейки C2 и на соответствующие значения ячеек С для отображения результата.

   Протяните столбик для вычисления результата по всем параметрам

Считаем долю от общего числа

Для начала разберем довольно распространенную ситуацию, когда нам нужно определить долю одного числа (в процентах) в другом. Ниже приведена математическая формула для выполнения данной задачи:

Доля (%) = Число 1/Число 2*100%, где:

• Число 1 – собственно говоря, наше исходное числовое значение
• Число 2 – итоговое число, долю в котором мы хотим выяснить

К примеру, давайте попробуем вычислить, какова доля числа 15 в числе 37. Результат нам нужен в процентах. В данном значение “Числа 1” равно 15, а “Числа 2” – 37.

1. Выбираем ячейку, где нам нужно произвести расчеты. Пишем знак “равно” (“=”) и далее формулу расчета с нашими числами: .
2. После того, как мы набрали формулу, нажимаем клавишу Enter на клавиатуре, и результат сразу же отобразится в выбранной ячейке.

У некоторых пользователей в результирующей ячейке вместо процентного значения может отобразится простое число, причем, иногда с большим количеством цифр после запятой.

Все дело в том, что не настроен формат ячейки для вывода результата. Давайте это исправим:

Кликаем правой кнопкой мыши по ячейке с результатом (неважно, до того, как мы написали в ней формулу и получили результат или после), в появившемся перечне команд щелкаем по пункту “Формат ячеек…”.
В окне форматирования мы окажемся во вкладке “Число”. Здесь в числовых форматах кликаем по строке “Процентный” и в правой части окна указываем желаемое количество знаков после запятой

Наиболее распространенный вариант – “2”, его мы и ставим в нашем примере. После этого жмем кнопку OK.
Готово, теперь мы получим в ячейке именно процентное значение, что и требовалось изначально.

Кстати, когда формат отображения в ячейке настроен в виде процентов, вовсе не обязательно в формуле писать “*100%“. Достаточно будет выполнить простое деление чисел: .

Давайте попробуем применить полученные знания на практике. Допустим, у нас есть таблица с продажами по различным наименованиям, и нам нужно вычислить долю каждого товара в суммарной выручке. Для удобства лучше вывести данные в отдельный столбец. Также, у нас должна быть заранее посчитана итоговая выручка по всем наименованиям, на которую мы будем делить продажи по каждому товару.

Итак, приступим к выполнению поставленной задачи:

1. Выбираем первую ячейку столбца (не считая шапку таблицы). Как обычно, написание любой формулы начинается со знака “=“. Далее пишем формулу расчета процента, аналогично рассмотренному примеру выше, только заменив конкретные числовые значения адресами ячеек, которые можно прописать вручную, либо добавляем их в формулу кликами мыши. В нашем случае, в ячейку E2 нужно написать следующее выражение: . Примечание: не забываем заранее настроить формат ячеек результирующего столбца, выбрав отображение в виде процентов.
2. Нажимаем Enter, чтобы получить результат в заданной ячейке.
3. Теперь нам нужно произвести аналогичные расчеты для остальных строк столбца. К счастью, возможности Эксель позволяют избежать ручного ввода формулы для каждой ячейки, и этот процесс можно автоматизировать путем копирования (растягивания) формулы в другие ячейки. Однако тут есть небольшой нюанс. В программе по умолчанию при копировании формул происходит корректировка адресов ячеек согласно смещению. Когда речь идет о продажах каждого отдельного наименования, так и должно быть, но координаты ячейки с итоговой выручкой должны оставаться неизменными. Чтобы ее зафиксировать (сделать абсолютной), нужно перед обозначениями строки и столбца добавить символ “$“. Либо, чтобы не печатать этот знак вручную, выделив адрес ячейки в формуле, можно просто нажать клавишу F4. По завершении нажимаем Enter.
4. Теперь осталось растянуть формулу на другие ячейки. Чтобы это сделать, наводим курсор на правый нижний угол ячейки с результатом, указатель должен поменять форму на крестик, после чего, растягиваем формулу вниз, зажав левую кнопку мыши.
5. Вот и все. Как мы и хотели, ячейки последнего столбца заполнились долями продаж каждого конкретного наименования продукции в совокупной выручке.

Разумеется, в расчетах вовсе не обязательно заранее считать итоговую выручку и выводить результат в отдельную ячейку. Все можно сразу посчитать с помощью одной формулы, которая для ячейки E2 выглядеть так: .

В данном случае, мы сразу посчитали общую выручку в формуле расчета доли, используя функцию СУММ. О том, как ее применять, читайте в нашей статье – “Как в Экселе посчитать сумму ячеек“.

Как и в первой варианте, нам нужно зафиксировать цифру по итоговым продажам, однако, так как в расчетах не принимает участие отдельная ячейка с нужным значением, нам нужно проставить знаки “$” перед обозначениями строк и столбцов в адресах ячеек диапазона суммы: .

Калькулятор Процентов

Что если % из ?		Результат:
это какой процент от ?		Ответ: %
это % от чего?		Ответ:

Как процентные соотношения помогают в реальной жизни

Есть два способа, как процентные соотношения помогают в решении наших каждодневных проблем:

1. Мы сравниваем две разных величины, когда все величины соотносятся с одной и той же основной величиной равной 100. Чтобы объяснить это, давайте рассмотрим следующий пример:

Пример:

Том открыл новую бакалейную лавку. За первый месяц он купил бакалеи за \$650 и продал за \$800, а во втором купил за \$800 и продал за \$1200. Надо рассчитать делает ли Том больше прибыли или нет.

Решение:

Напрямую из этих чисел мы не можем сказать растёт доход Тома или нет, потому что расходы и выручка каждый месяц разные. Для того, чтобы решить эту задачу, нам нужно соотнести все значения к фиксированной основной величине равной 100. Давайте выразим процентное соотношение его доходов к расходам в первый месяц:

(800 — 650) ÷ 650 ⋅ 100 = 23,08%

Это значит, что если Том тратил \$100, то он делал прибыль в размере 23.08 в первый месяц.

Теперь давайте применим тоже самое ко второму месяцу:

(1200 — 800) ÷ 800 ⋅ 100 = 50%

Так, во втором месяце, если Том тратил \$100, то его доход был \$50(потому что \$100⋅50% = \$100⋅50÷100=\$50). Теперь понятно,что доходы Тома растут.

2. Мы можем определять количество части большей величины, если известно процентное соотношение этой части. Чтобы объяснить это, давайте рассмотрим следующий пример:

Пример:

Синди хочет купить 8 метров шланга для своего сада. Она пошла в магазин и обнаружила, что там есть катушка со шлангом длиной 30 метров. Однако, она заметила, что на катушке написано, что 60% уже продано. Она должна узнать хватит ли ей оставшегося шланга.

Решение:

В табличке сказано, что

$\frac{Продано\ длина}{Всего\ длина} \times 100 = 60\%$

$Продано\ длина = \frac{60 \times 30}{100} = 18м$

Поэтому остаток 30 — 18 = 12м, которого вполне достаточно Синди.

Примеры:

1. Райн любит собирать спортивные карточки с его любимыми игроками. У него есть 32 карточки с игроками бейсбола, 25 карточки с футболистами и 47 с баскетболистами. Каково процентное соотношение карточек каждого спорта в его коллекции?

Решение:

Общее количество карточек = 32 + 25 + 47 = 104

Процентное соотношение бейсбольных карточек = 32/104 x 100 = 30,8%

Процентное соотношение футбольных карточек = 25/104 x 100 = 24%

Процентное соотношение баскетбольных карточек = 47/104 x 100 = 45,2%

Обратите внимание, что если сложить все проценты, то получится 100%, что представляет общее количество карточек. 2

На уроке был математический тест. Тест состоял из 5 вопросов; за три из них давали по три 3 балла за каждый, а за осташиеся два — по четыре балла. Вам удалось правильно ответить на два вопроса по 3 балла и на один вопрос по 4 балла. Какое процентное соотношение баллов Вы получили за этот тест?

2. На уроке был математический тест. Тест состоял из 5 вопросов; за три из них давали по три 3 балла за каждый, а за осташиеся два — по четыре балла. Вам удалось правильно ответить на два вопроса по 3 балла и на один вопрос по 4 балла. Какое процентное соотношение баллов Вы получили за этот тест?

Решение:

Общее количество = 3×3 + 2×4 = 17 баллов

Полученные балы = 2×3 + 4 = 10 баллов

Процентное соотношение полученных баллов = 10/17 x 100 = 58,8%

3. Вы купили видео игру за \$40. Потом цены на эти игры подняли на 20%. Какова новая цена видео игры?

Решение:

Увеличение цены равно 40 x 20/100 = \$8

Новая цена равна 40 + 8 = \$48

Процентное соотношение (или отношение) двух чисел — это отношение одного числа к другому умноженное на 100%.

Процентное отношение двух чисел можно записать следующей формулой:

Онлайн-сервисы для вычислений

В нахождении нужных процентов могут помочь различные сервисы-калькуляторы, работающие в режиме онлайн. Например, популярный сайт fin-calc.org.ua имеет в своём функционале различные инструменты, помогающие, в том числе, высчитать процент от любого числа.

1. Перейдите на fin-calc.org.ua.
2. Введите искомые показатели в соответствующие клетки.
3. Нажмите на «Рассчитать». Вы сразу же получите искомый результат.

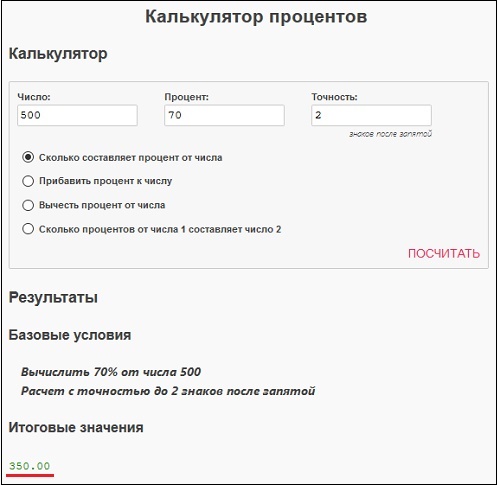
Калькуляционные вычисления на fin-calc.org.ua

Также указанный калькулятор позволяет высчитать какую долю от 1 составляет 2, прибавить % к числу или вычесть из него. Всё очень быстро и удобно.

Как просчитать процент на калькуляторе

Затем в поля нужно ввести запрашиваемые данные и получить результат. При этом можно узнать, как % от общего числа, так и сколько процентов составляет значение одного числа от другого.Подводя итоги, можно сказать, что калькулятор позволяет определиться с такими вопросами:

1. Вычислить определенный % из определенного значения. Или, если известен %, то прибавить его к какому-то числу.
2. Какой % составляет от заданного показателя.
3. Сколько % содержит одно значение от другого.

На обычном калькуляторе также есть функция определения %. Если опция есть, то должна быть клавиша, где изображен %.

Для этого найдите на его клавиатуре кнопку с изображением процента (%).

Для этого проведем следующие манипуляции:

Введите 125 на калькуляторе. Нажмите умножить (*). Нажмите 12. Затем нажмите кнопку с процентом. При этом на экране отобразиться результат – 9,6%.

Таким образом, можно найти любые другие значения с двумя числами. Калькулятором можно и воспользоваться на мобильном телефоне.

В ноутбуке или компьютере полезную программку можно отыскать через меню пуск.

Увеличение/Уменьшение процентного соотношения

Когда число увеличивается относительно другого числа, то величина увеличения представляется как:

Увеличение = Новое число — Старое число

Однако, когда число уменьшается относительно другого числа, то эту величину можно представить как:

Уменьшение = Старое число — Новое число

Увеличение или уменьшение числа всегда выражается на основании старого числа.Поэтому:

%Увеличение = 100 ⋅ (Новое число — Старое число) ÷ Старое число

%Уменьшение = 100 ⋅ (Старое число — Новое число) ÷ Старое число

Например, у Вас было 80 почтовых марок и Вы начали в этом месяце собирать ещё пока общее количество почтовых марок достигло 120. Процентное увеличение числа марок, которые у Вас есть равно

$\frac{120 — 80}{80} \times 100 = 50\%$

Когда у Вас стало 120 марок, Вы и Ваш друг договорились обменять игру «Lego» на несколько из этих марок. Ваш друг взял несколько марок, которые ему понравились, и когда Вы подсчитали оставшиеся марки, то обнаружили, что у Вас осталось 100 марок. Процентное уменьшение числа марок может быть подсчитано как:

$\frac{120 — 100}{120} \times 100 = 16,67\%$

Способ второй: переводим проценты в десятичную дробь

Как вы помните, процент — сотая часть числа. В виде десятичной дроби это 0,01 (ноль целых одна сотовая). Следовательно, 17% – это 0,17 (ноль целых, семнадцать сотых), 45% – 0,45 (ноль целых, сорок пять сотых) и т. д. Полученную десятичную дробь умножаем на сумму, процент от которой считаем. И находим искомый ответ.

Например, давайте рассчитаем сумму подоходного налога от зарплаты 35 000 рублей. Налог составляет 13%. В виде десятичной дроби это будет 0,13 (ноль целых, тринадцать сотых). Умножим сумму 35 000 на 0,13. Получится 4 550. Значит, после вычета подоходного налога вам будет перечислена зарплата 35 000 – 4 550 = 30 050. Иногда эту сумму уже без налога называют «зарплатой на руки» или «чистой». В противовес этому сумму вместе с налогом «грязной зарплатой». Именно «грязную зарплату» указывают в объявлениях о вакансиях компании и в трудовом договоре. На руки же даётся меньше. Сколько? Теперь вы легко посчитаете.