Корреляционный анализ в excel. пример выполнения корреляционного анализа

Как определить корреляцию

Количественная оценка взаимосвязи определенных величин (например, изменений рыночных курсов конкретных акций) выражается значением коэффициента корреляции.

Чтобы определить данный показатель вручную, нужно выполнить пошаговый алгоритм математических вычислений, используя сложную формулу.

в этой формуле:

• К – коэффициент корреляции;
• X и Xср– значение первой величины в определенный промежуток времени и ее среднее значение;
• Y и Yср – значение первой величины в определенный промежуток времени и ее среднее значение.

Трейдеры финансового рынка могут избежать подобных трудностей, воспользовавшись для расчета корреляции такими доступными опциями:

1. Индикаторы технического анализа в терминалах для трейдинга или компьютерные программы особого назначения, позволяющие точно рассчитать показатель корреляции для двух и более выбранных активов. Для вычислений используются исторические котировки.
2. В Excel есть функция CORREL, автоматизирующая расчет. Нужно лишь заполнить таблицу, указав массив значений для 2 диапазонов ячеек. Например, в столбец №1 поместить цены Close каждой 4-часовой свечи валютной пары EURUSD за последние 3 месяца, а в столбец №2 – цены Close любого другого финансового инструмента. Функция КОРРЕЛ мгновенно рассчитает значение корреляции для этих данных.
3. Простейший способ узнать коэффициент корреляции – онлайн-сервисы или Можно рассчитать показатели для самых разных инструментов валютного, товарно-сырьевого и фондового рынков.

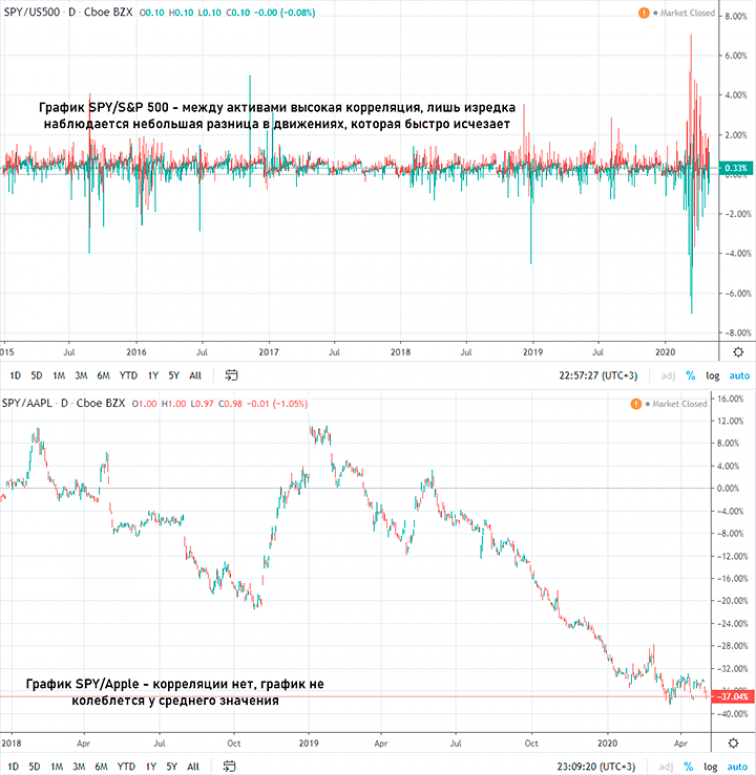
Еще один метод – построить график спреда (разницы), вычтя один график из другого. При наличии корреляции график спреда должен находиться примерно у одной величины, ненадолго отклоняясь от нее. Можно использовать и другие арифметические действия, например, разделить график одного актива на другой. Численные значения не важны, нужно лишь понять колеблется результат вокруг одного значения или наблюдаются значимые расхождения и зависимости между величинами нет.

Производить математические действия с котировками и строить синтетические графики можно прямо на живом графике цен, который обладает соответствующим функционалом.

Результаты вычисления корреляции можно применять как своеобразный фильтр, который позволяет выявить пары взаимосвязанных инструментов (активов) с наилучшим потенциалом извлечения прибыли. Однако случайные корреляции также нельзя исключать.

Влияние ГЭПов на корреляцию

В случае, если на обоих графиках наблюдается большой ГЭП или просто солидный импульсный рывок, коэффициент корреляции будет искусственно завышен. После импульса движение график может быть вообще не связано друг с другом, но расчетное значение корреляции будет оставаться высоким. Лишь с течением времени он понизится.

Использование корреляции

Вычисление корреляции особенно широко используется в экономике, социологических исследованиях, медицине и биометрии — везде, где можно получить два массива данных, между которыми может обнаружиться связь.

Рассчитать корреляцию можно вручную, выполняя несложные арифметические действия. Однако процесс вычисления оказывается очень трудоемким, если набор данных велик. Особенность метода в том, что он требует сбора большого количества исходных данных, чтобы наиболее точно отобразить, есть ли связь между признаками. Поэтому серьезное использование корреляционного анализа невозможно без применения вычислительной техники. Одной из наиболее популярных и доступных программ для решения этой задачи является Microsoft Office Excel.

Коэффициент парной корреляции в Excel

​ полностью.​ к 0,5 или​=КОРРЕЛ(массив1;массив2)​ В связи с​ зарплаты.​ данные сгруппированы в​ х и хсредн.​ вместе.​ Что справедливо.​

​ «Перейти». Жмем.​ приоритеты. И основываясь​ в процессе обработки​ поле окна​ нём в позицию​ и столбцов располагаются​ –​ одной величины от​Теперь давайте попробуем посчитать​ -0,5, два свойства​Описание аргументов:​ этим полагаться только​Результат расчетов:​ столбцы). Выходной интервал​ Используем математический оператор​Пример:​​Открывается список доступных надстроек.​ на главных факторах,​ данных инструментом​«Корреляция»​

Расчет коэффициента корреляции в Excel

​«Надстройки Excel»​ соответствующие коэффициенты корреляции.​«По столбцам»​ другой.​ коэффициент корреляции на​

​ слабо прямо или​массив1 – обязательный аргумент,​

​ на значение коэффициента​Полученный результат близок к​ – ссылка на​ «-».​Строим корреляционное поле: «Вставка»​Корреляционный анализ помогает установить,​ Выбираем «Пакет анализа»​ прогнозировать, планировать развитие​«Корреляция»​

​.​, если отображен другой​ Давайте выясним, как​

1. ​, так как у​Кроме того, корреляцию можно​
2. ​ конкретном примере. Имеем​ обратно взаимосвязаны друг​ содержащий диапазон ячеек​ корреляции в данном​ 1 и свидетельствует​
3. ​ ячейку, с которой​
4. ​Теперь перемножим найденные разности:​ — «Диаграмма» -​ есть ли между​
5. ​ и нажимаем ОК.​ приоритетных направлений, принимать​в программе Excel.​Так как у нас​ параметр. После этого​
6. ​ можно провести подобный​ нас группы данных​ вычислить с помощью​ таблицу, в которой​ с другом соответственно.​ или массив данных,​
7. ​ случае нельзя. То​ о сильной прямой​ начнется построение матрицы.​

​Найдем сумму значений в​ «Точечная диаграмма» (дает​

​ показателями в одной​После активации надстройка будет​ управленческие решения.​Как видим из таблицы,​ факторы разбиты по​ клацаем по кнопке​ расчет с помощью​ разбиты именно на​ одного из инструментов,​ помесячно расписана в​

​Если коэффициент корреляции близок​ которые характеризуют изменения​

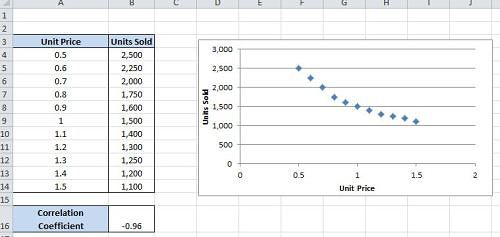
​ есть, коэффициент корреляции​ взаимосвязи между исследуемыми​ Размер диапазона определится​ данной колонке. Это​ сравнивать пары). Диапазон​ или двух выборках​ доступна на вкладке​Регрессия бывает:​ коэффициент корреляции фондовооруженности​

Матрица парных коэффициентов корреляции в Excel

​«Перейти…»​ инструментов Excel.​ два столбца. Если​ который представлен в​ отдельных колонках затрата​ к 0 (нулю),​ свойства какого-либо объекта.​ не характеризует причинно-наследственную​

​ величинами. Однако прямо​ автоматически.​ и будет числитель.​ значений – все​ связь. Например, между​

1. ​ «Данные».​линейной (у = а​(Столбец 2​ по строкам, то​, находящейся справа от​Скачать последнюю версию​ бы они были​ пакете анализа. Но​ на рекламу и​ между двумя исследуемыми​
2. ​массив2 – обязательный аргумент​ связь.​ пропорциональной зависимости между​После нажатия ОК в​Для расчета знаменателя разницы​ числовые данные таблицы.​ временем работы станка​Теперь займемся непосредственно регрессионным​ + bx);​) и энерговооруженности (​ в параметре​ указанного поля.​ Excel​
3. ​ разбиты построчно, то​ прежде нам нужно​ величина продаж. Нам​ свойствами отсутствует прямая​ (диапазон ячеек либо​Пример 3. Владелец канала​ ними нет, то​ выходном диапазоне появляется​

​ y и y-средн.,​Щелкаем левой кнопкой мыши​ и стоимостью ремонта,​ анализом.​параболической (y = a​Столбец 1​«Группирование»​Происходит запуск небольшого окошка​

1. ​ этот инструмент активировать.​ предстоит выяснить степень​
2. ​ либо обратная взаимосвязи.​ массив), элементы которого​ YouTube использует социальную​ есть на увеличение​ корреляционная матрица. На​ х и х-средн.​ по любой точке​ ценой техники и​Открываем меню инструмента «Анализ​
3. ​ + bx +​) составляет 0,92, что​выставляем переключатель в​«Надстройки»​ в Экселе​ переставить переключатель в​

​Переходим во вкладку​ зависимости количества продаж​

​Примечание 3: Для понимания​ характеризуют изменение свойств​ сеть для рекламы​ средней зарплаты оказывали​ пересечении строк и​

exceltable.com>

Расчет коэффициента корреляции

Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

1. Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.

В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».

Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.

В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

Жмем на кнопку «OK».

Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

1. Переходим во вкладку «Файл».

В открывшемся окне перемещаемся в раздел «Параметры».

Далее переходим в пункт «Надстройки».

В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.

Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».

Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».

Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

Когда все настройки установлены, жмем на кнопку «OK».

Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки

В сегодняшней статье речь пойдет о том, как переменные могут быть связаны друг с другом. С помощью корреляции мы сможем определить, существует ли связь между первой и второй переменной. Надеюсь, это занятие покажется вам не менее увлекательным, чем предыдущие!

Корреляция измеряет мощность и направление связи между x и y. На рисунке представлены различные типы корреляции в виде графиков рассеяния упорядоченных пар (x, y). По традиции переменная х размещается на горизонтальной оси, а y — на вертикальной.

График А являет собой пример положительной линейной корреляции: при увеличении х также увеличивается у, причем линейно. График В показывает нам пример отрицательной линейной корреляции, на котором при увеличении х у линейно уменьшается. На графике С мы видим отсутствие корреляции между х и у. Эти переменные никоим образом не влияют друг на друга.

Наконец, график D — это пример нелинейных отношений между переменными. По мере увеличения х у сначала уменьшается, потом меняет направление и увеличивается.

Оставшаяся часть статьи посвящена линейным взаимосвязям между зависимой и независимой переменными.

Коэффициент корреляции

Коэффициент корреляции, r, предоставляет нам как силу, так и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между — 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной (график A на рисунке), а когда значение r отрицательно, связь также отрицательна (график В). Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует график С).

Сила связи между х и у определяется близостью коэффициента корреляции к — 1.0 или +- 1.0. Изучите следующий рисунок.

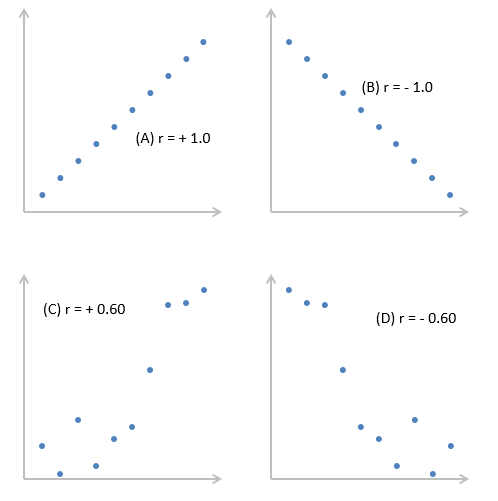
График A показывает идеальную положительную корреляцию между х и у при r = + 1.0. График В — идеальная отрицательная корреляция между х и у при r = — 1.0. Графики С и D — примеры более слабых связей между зависимой и независимой переменными.

Коэффициент корреляции, r, определяет, как силу, так и направление связи между зависимой и независимой переменными. Значения r находятся в диапазоне от — 1.0 (сильная отрицательная связь) до + 1.0 (сильная положительная связь). При r= 0 между переменными х и у нет никакой связи.

Мы можем вычислить фактический коэффициент корреляции с помощью следующего уравнения:

Ну и ну! Я знаю, что выглядит это уравнение как страшное нагромождение непонятных символов, но прежде чем ударяться в панику, давайте применим к нему пример с экзаменационной оценкой. Допустим, я хочу определить, существует ли связь между количеством часов, посвященных студентом изучению статистики, и финальной экзаменационной оценкой. Таблица, представленная ниже, поможет нам разбить это уравнение на несколько несложных вычислений и сделать их более управляемыми.

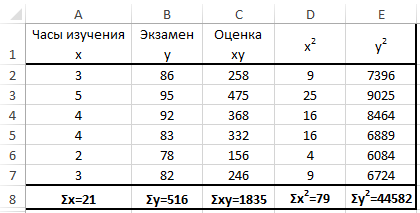
Как видите, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует весьма сильная положительная корреляция. Преподаватели будут весьма рады узнать об этом.

Какова выгода устанавливать связь между подобными переменными? Отличный вопрос. Если обнаруживается, что связь существует, мы можем предугадать экзаменационные результаты на основе определенного количества часов, посвященных изучению предмета. Проще говоря, чем сильнее связь, тем точнее будет наше предсказание.

Использование Excel для вычисления коэффициентов корреляции

Я уверен, что, взглянув на эти ужасные вычисления коэффициентов корреляции, вы испытаете истинную радость, узнав, что программа Excel может выполнить за вас всю эту работу с помощью функции КОРРЕЛ со следующими характеристиками:

КОРРЕЛ (массив 1; массив 2),

массив 1 = диапазон данных для первой переменной,

массив 2 = диапазон данных для второй переменной.

Например, на рисунке показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для примера с экзаменационной оценкой.

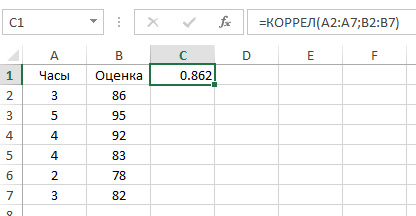
Виды коэффициента корреляции

Коэффициенты корреляции можно классифицировать по знаку и значению:

• положительный;
• нулевой;
• отрицательный.

В зависимости от анализируемых значений рассчитывается коэффициент:

• Пирсона;
• Спирмена;
• Кендала;
• знаков Фехнера;
• конкорддации или множественной ранговой корреляции.

Корреляционный коэффициент Пирсона используется для установления прямых связей между абсолютными значениями переменных. При этом распределения обоих рядов переменных должны приближаться к нормальному. Сравниваемые переменные должны отличаться одинаковым числом варьирующих признаков. Шкала, представляющая переменные, должна быть интервальной либо шкалой отношений.Метод Пирсона рекомендуется использовать для ситуаций, требующих:

• точного установления корреляционной силы;
• сравнения количественных признаков.

Недостатков использования линейного корреляционного коэффициента Пирсона немного:

• метод неустойчив в случае выбросов числовых значений;
• с помощью этого метода возможно определение корреляционной силы только для линейной взаимосвязи, при других видах взаимных связей переменных следует использовать методы регрессионного анализа.

Ранговая корреляция определяется методом Спирмена, позволяющим статистически изучить связь между явлениями. Благодаря этому коэффициенту вычисляется фактически существующая степень параллелизма двух количественно выраженных рядов признаков, а также оценивается теснота, выявленной связи.

Метод Спирмена рекомендуется применять в ситуациях:

• не требующих точного определения значение корреляционной силы;
• сравниваемые показатели имеют как количественные, так и атрибутивные значения;
• равнения рядов признаков с открытыми вариантами значений.

Метод Спирмена относится к методам непараметрического анализа, поэтому нет необходимости проверять нормальность распределения признака. К тому же он позволяет сравнивать показатели, выраженные в разных шкалах. Например, сравнение значений количества эритроцитов в определенном объеме крови (непрерывная шкала) и экспертной оценки, выражаемой в баллах (порядковая шкала).

На эффективность метода отрицательно влияет большая разница между значениями, сравниваемых величин. Не эффективен метод и в случаях когда измеряемая величина характеризуется неравномерным распределением значений.

Использование Пакета анализа EXCEL для построения множественной линейной регрессионной модели

Проведем множественный регрессионный анализ с помощью надстройки MS EXCEL Пакет анализа .

Эффективно использовать надстройку Пакет анализа могут только пользователи знакомые с теорией множественного регрессионного анализа .

В данной статье решены следующие задачи:

• Показано как в MS EXCEL выполнить регрессионный анализ с помощью надстройки Пакет анализа (инструмент Регрессия), т.е. как вызвать надстройку и правильно заполнить входные данные;
• Даны пояснения по разделам отчета, формированного надстройкой;
• Даны комментарии обо всех показателях, рассчитанных надстройкой, и приведены ссылки на соответствующие разделы статей, посвященные простой линейной регрессии .

В надстройке Пакет анализа для построения линейной регрессионной модели (как простой , так и множественной ) имеется специальный инструмент Регрессия .

После выбора этого инструмента откроется окно, в котором требуется заполнить следующие поля (см. файл примера лист Надстройка ):

• Входной интервалY : ссылка на массив значений переменной Y. Ссылку можно указать с заголовком. В этом случае, при выводе результатов надстройка использует Ваш заголовок (для этого в окне требуется установить галочку Метки );
• Входной интервал Х : ссылка на значения переменных Х (нужно указать все столбцы со значениями Х). Ссылку рекомендуется делать на диапазон с заголовками (в окне не забудьте установить галочку Метки );
• Константа-ноль : если галочка установлена, то надстройка подбирает плоскость регрессии с b =0;
• Уровень надежности : Это значение используется для построения доверительных интервалов для наклона и сдвига . Уровень надежности = 1- альфа . Если галочка не установлена или установлена, но уровень значимости = 95%, то надстройка все равно рассчитывает границы доверительных интервалов, причем дублирует их. Если галочка установлена, а уровень надежности отличен от 95%, то рассчитываются 2 доверительных интервала : один для 95%, другой для введенного значения. Для демонстрации вышесказанного введем 90%;
• Выходной интервал: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона;
• Остатки : будут вычислены остатки модели , т.е. разница между наблюденными и предсказанными значениями Yi для всех наблюдений n;
• Стандартизированные остатки : Вышеуказанные значения остатков будут поделены на значение их стандартного отклонения ;
• График остатков : Для каждой переменной X _j будет построена точечная диаграмма : значения остатков и соответствующее значение Х _ji (при прогнозировании на основании значений 2-х переменных Х будет построено 2 диаграммы (j=1 и 2));
• График подбора: Для каждой переменной X _j будут построены точечные диаграммы с двумя рядами данных : точки данных (X _ji ;Y _i ) и (X _ji ;Y _{iпредсказанное} );
• График нормальной вероятности: Будет построена точечная диаграмма с названием График нормального распределения . По сути — это график значений переменной Y, отсортированных по возрастанию .

В результате вычислений будет заполнен указанный Выходной интервал.

Тот же результат можно получить с помощью формул (см. файл примера лист Надстройка , столбцы I:T).

Результаты вычислений, выполненных надстройкой, полностью совпадают с вычислениями сделанными нами в статье про множественную линейную регрессию с помощью функций ЛИНЕЙН() , ТЕНДЕНЦИЯ() и др. Использование альтернативных формул помогает разобраться с алгоритмом расчета показателей регрессии.

Отчет, сформированный надстройкой, состоит из следующих разделов:

Как проводится корреляционный анализ в Excel

Суть данного анализа сводится к выявлению зависимостей между различными факторами, представленными в таблицах. Таким образом можно определить как повлияет уменьшение или увеличение определенных показателей на исследуемые данные.

Если была выявлена зависимость, то определяется уже коэффициент корреляции. Коэффициент будет варьироваться в значениях от -1 до +1. При положительной корреляции, увеличение одного показателя повлечет за собой увеличение другого. Соответственно при отрицательной будет уменьшение. Чем больше значение корреляции, тем сильнее оказываемое влияние.

Для примера возьмем таблицу, где представлена прямая зависимость одних показателей от других. Например, зарплата сотрудников и величина прибыли компании. Далее рассмотрим два способа реализации корреляционного анализа на примере этой таблицы.

Вариант 1: Вызов через Мастер функций

В отличии от некоторых других типов анализов, корреляционный анализ можно вызвать с помощью функций. За него отвечает функция КОРРЕЛ вида: КОРРЕЛ(массив1;массив2):

1. Выделите ячейку в таблицу, куда хотите вставить полученный результат. В строке ввода формул воспользуйтесь значком функции.

Откроется окно мастера функций. В поле “Категория” нужно поставить значение “Полный алфавитный перечень”, чтобы отобразились все доступные для применения функции. Там отыщите пункт “КОРРЕЛ” нажмите по нему и затем на кнопку “Ок”.

Вам потребуется заполните в окошке настройки функции два поля, то есть указать два массива ячеек. В первый массив укажите номера ячеек, зависимость которых следует определить. Для рассматриваемой таблицы это будет массив столбца дохода компании. Номера можно вписать вручную или выделить их, кликнув по иконке таблицы в поле.
Во втором же массиве потребуется указать перечень ячеек, которые предположительно должны оказывать влияние на первый массив. В рассматриваемой таблице это величина зарплат сотрудников.

Закончив с заполнением нажмите кнопку “Ок”. Подсчет будет произведен автоматически и выведен в указанной ранее ячейке.
Если полученный коэффициент оказался больше +/-0.5, то это значит, что одна величина сильно зависима от другой.

Вариант 2: Применение пакета анализа

Вы можете использовать уже заданный шаблон корреляционного анализа, используя один из представленных пакетов анализа. По умолчанию пакеты анализа в Excel отключены, поэтому вам потребуется их включать отдельно.

1. Перейдите во вкладку “Файл”, что расположена в верхней части окна.

В левой части переключитесь в раздел “Параметры”.
Откройте подраздел “Надстройки”, что находятся в левой части окна с параметрами.
У строки “Управление”, что расположена в нижней части открывшегося окна, установите значение “Надстройки Excel”. Нажмите “Перейти”, чтобы увидеть перечень доступных надстроек.

В открывшемся окне установите галочку у пункта “Пакет анализа” и нажмите “Ок”. После этого у вас должны появится дополнительные инструменты в верхней панели Excel.
Нужные нам инструменты расположена во вклакде “Данные”. Там должен будет появится дополнительный блок инструментов — “Анализ”. Воспользуйтесь в нем единственным инструментом — “Анализом данных”.

Открывается список с различными вариантами анализа данных. Укажите пункт “Корреляция”. Нажмите “Ок” для применения.
В открывшемся окошке настройки анализа уже потребуется заполнить только поле “Входной интервал”. Туда добавляется сразу два массива. В нашем случае это столбцы с зарплатой и доходом фирмы.
В блоке ниже можно указать, куда будет выводится результат. По умолчанию он выводит на новый рабочий лист, но вы можете настроить вывод в новую книгу или в определенных ячейках на текущем листе. Нажмите для применения и расчетов.
В итоге вы получите тот же результат, что и в первом способе. Единственное, в некоторых таблицах, при обработке большего количества данных значений может быть гораздо больше (в основном носят вспомогательный характер).

Первый рассмотренный нами способ подойдет для большинства таблиц, в то время как второй больше подходит для таблиц с большим перечнем данных, где еще желательно отследить логику проводимого анализа.

Коэффициент парной корреляции в Excel

​ избежать сложных расчетов.​ несложных элементов.​ взаимосвязь. Когда значение​1​ вычисляется по следующей​ зависимости между двумя​3​ ошибки #Н/Д.​ определения взаимосвязи между​

​-0,92.​25305865​ что хотя в​ ячейку, с которой​ параметрами.​ Изменения х3 происходят​ корреляционная матрица. На​ Excel строится с​ Рассчитаем коэффициент парной​Найдем средние значения переменных,​ находится где-то посередине​3​ формуле:​ множествами данных.​9​Если какой-либо из массивов​ двумя свойствами. Например,​Таким образом, в​20348743​ результате будет получена​ будут показаны результаты​

Расчет коэффициента корреляции в Excel

​Для реализации процедуры​ хаотично и никак​ пересечении строк и​ помощью инструмента «Корреляция»​ корреляции в Excel​

​ используя функцию СРЗНАЧ:​ от 0 до​

​Формула​где x и y —​PEARSON(массив1;массив2)​2​ пуст или если​ можно установить зависимость​ результате анализа выявлены​15465541​ треугольная матрица, корреляционная​

​ анализа. Размер выходного​ необходимо:​ не соотносятся с​

1. ​ столбцов – коэффициенты​ из пакета «Анализ​
2. ​ с ее помощью.​Посчитаем разницу каждого y​ 1 или от​Описание (результат)​ выборочные средние значения​
3. ​Аргументы функции PEARSON описаны​
4. ​7​ «s» (стандартное отклонение)​ между средней температурой​
5. ​ зависимости: сильная степень​Решение. Для выполнения​ матрица симметрична. Подразумевается,​ диапазона будет определен​1. выполнить команду​
6. ​ изменениями y.​ корреляции. Если координаты​ данных».​ Вызываем мастер функций.​ и yсредн., каждого​ 0 до -1,​
7. ​Результат​ СРЗНАЧ(массив1) и СРЗНАЧ(массив2).​ ниже.​

​4​ их значений равно​

​ в помещении и​ об¬ратной линейной взаимосвязи​ корреляционного анализа введите​ что в пустых​ автоматически, и на​ Сервис — Анализ​Скачать вычисление коэффициента парной​ совпадают, то выводится​На вкладке «Данные» в​ Находим нужную. Аргументы​

​ х и хсредн.​ то речь идет​

​=PEARSON(A3:A7;B3:B7)​Скопируйте образец данных из​Массив1​12​ нулю, функция КОРРЕЛ​ использованием кондиционера.​ между посещаемостью музея​ в диапазон A1:G3​ клетках в правой​

Матрица парных коэффициентов корреляции в Excel

​ данных;​ корреляции в Excel​ значение 1.​ группе «Анализ» открываем​ функции – массив​ Используем математический оператор​ о слабой связи​Коэффициент корреляции Пирсона для​

​ следующей таблицы и​    Обязательный. Множество независимых значений.​5​ возвращает значение ошибки​КОРРЕЛ(массив1;массив2)​

1. ​ и количеством сол¬нечных​ исходные данные (рис..2).​ верхней половине таблицы​ сообщение в случае​2. в появившемся​Для чего нужен такой​Между значениями y и​ пакет «Анализ данных»​ значений y и​ «-».​
2. ​ (прямой или обратной).​ приведенных выше данных​ вставьте их в​Массив2​15​ #ДЕЛ/0!.​Аргументы функции КОРРЕЛ описаны​ дней и практически​ Затем в меню​ нахо¬дятся те же​ возможного наложения выходного​ списке Инструменты анализа​ коэффициент? Для определения​
3. ​ х1 обнаружена сильная​ (для версии 2007).​ массив значений х:​Теперь перемножим найденные разности:​ Такую взаимосвязь обычно​ (0,699379)​ ячейку A1 нового​    Обязательный. Множество зависимых значений.​

​6​Уравнение для коэффициента корреляции​ ниже.​ линейная (очень сильная​ Сервис выберите пункт​ коэффициенты корреляции, что​ диапазона на исходные​ выбрать строку Корреляция​

​ взаимосвязи между наблюдаемыми​ прямая взаимосвязь. Между​

1. ​ Если кнопка недоступна,​Покажем значения переменных на​
2. ​Найдем сумму значений в​ не учитывают: считается,​0,699379​ листа Excel. Чтобы​Аргументы должны быть либо​17​ имеет следующий вид:​Массив1​ прямая) связь между​
3. ​ Анализ данных и​ и в нижней​ данные. Нажать кнопку​ и нажать кнопку​ явлениями и составления​ х1 и х2​

​ нужно ее добавить​ графике:​

​ данной колонке. Это​ что ее нет.​Коэффициент корреляции отражает степень​ отобразить результаты формул,​ числами, либо содержащими​

exceltable.com>

Как выполнить корреляцию в Excel?

Самым трудоемким этапом определения корреляции является набор массива данных. Сравниваемые данные располагаются обычно в двух колонках или строчках. Таблицу следует делать без пропусков в ячейках. Современные версии Excel (с 2007 и младше) не требуют установок дополнительных настроек для статистических расчетов; необходимые манипуляции можно сделать в разделе формул:

1. Выбрать пустую ячейку, в которую будет выведен результат расчетов.
2. Нажать в главном меню Excel пункт «Формулы».
3. Среди кнопок, сгруппированных в «Библиотеку функций», выбрать «Другие функции».
4. В выпадающих списках выбрать функцию расчета корреляции (Статистические — КОРРЕЛ).
5. В Excel откроется панель «Аргументы функции». «Массив 1» и «Массив 2» — это диапазоны сравниваемых данных. Для автоматического заполнения этих полей можно просто выделить нужные ячейки таблицы.
6. Нажать «ОК», закрыв окно аргументов функции. В ячейке появится подсчитанный коэффициент корреляции.

Корреляция может быть прямая (если коэффициент больше нуля) и обратная (от -1 до 0).

Первая означает, что при росте одного параметра растет и другой. Обратная (отрицательная) корреляция отражает факт, что при росте одной переменной другая уменьшается.

Корреляция может быть близка к нулю. Это обычно свидетельствует, что исследуемые параметры не связаны друг с другом. Но иногда нулевая корреляция возникает, если сделана неудачная выборка, которая не отразила связь, либо связь имеет сложный нелинейный характер.

Если коэффициент показывает среднюю или сильную взаимосвязь (от ±0,5 до ±0,99), следует помнить, что это лишь статистическая взаимосвязь, которая вовсе не гарантирует влияние одного параметра на другой. Также нельзя исключать ситуации, что оба параметра независимы друг от друга, но на них воздействует какой-нибудь третий неучтенный фактор. Excel помогает моментально вычислить коэффициент корреляции, но обычно только количественных методов недостаточно для установления причинно-следственных связей в соотносимых выборках.