Как использовать функцию reshape() библиотеки numpy в python

Аудио и временные ряды в NumPy

По сути аудио файл  — это одномерный массив семплов. Каждый семпл представляет собой число, которое является крошечным фрагментов аудио сигнала. Аудио CD-качества может содержать 44 100 семплов в секунду, каждый из которых является целым числом в промежутке между -32767 и 32768. Это значит, что десятисекундный WAVE-файл CD-качества можно поместить в массив NumPy длиной в 10 * 44 100 = 441 000 семплов.

Хотите извлечь первую секунду аудио? Просто загрузите файл в массив NumPy под названием , после чего получите .

Фрагмент аудио файла выглядит следующим образом:

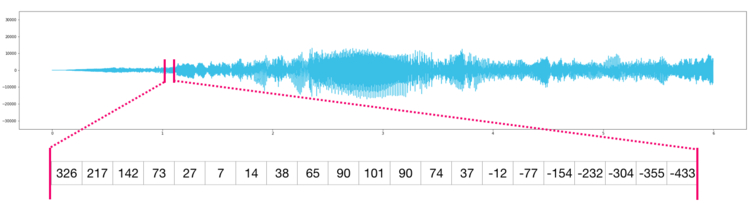
То же самое касается данных временных рядов, например, изменения стоимости акций со временем.

Функция Numpy mgrid() v/s meshgrid() в Python

Numpy mgrid() конкретизирует заданные индексы, транслируя их в виде плотных сеток. Одновременно функция meshgrid() полезна для создания массивов координат. Векторизация оценок функций по сетке. Функция Meshgrid() вдохновлена MATLAB. Кроме того, meshgrid() создает прямоугольную сетку из двух заданных одномерных массивов, представляющих декартовы индексы.

Пример функции Numpy meshgrid ():

import numpy as np 
.linspace(-4, 4, 9) 
  
# numpy.linspace creates an array of 9 linearly placed elements between -4 and 4, both inclusive  
.linspace(-5, 5, 11) 
  
x_1,.meshgrid(x, y) 
  y_1 = ") 
print(y_1)

Выход:

x_1 = 

 
 
 
 
 
 
 
 
 
 ]
y_1 = 

 
 
 
 
 
 
 
 
 
 ]

1.4.1.4. Basic visualization¶

Now that we have our first data arrays, we are going to visualize them.

Start by launching IPython:

$ ipython # or ipython3 depending on your install

Or the notebook:

$ jupyter notebook

Once IPython has started, enable interactive plots:

>>> %matplotlib  

Or, from the notebook, enable plots in the notebook:

>>> %matplotlib inline 

The is important for the notebook, so that plots are displayed in
the notebook and not in a new window.

Matplotlib is a 2D plotting package. We can import its functions as below:

>>> import matplotlib.pyplot as plt  # the tidy way

And then use (note that you have to use explicitly if you have not enabled interactive plots with ):

>>> plt.plot(x, y)       # line plot    
>>> plt.show()           # <-- shows the plot (not needed with interactive plots) 

Or, if you have enabled interactive plots with :

>>> plt.plot(x, y)       # line plot    

1D plotting:

>>> x = np.linspace(, 3, 20)
>>> y = np.linspace(, 9, 20)
>>> plt.plot(x, y)       # line plot    

>>> plt.plot(x, y, 'o')  # dot plot    

2D arrays (such as images):

>>> image = np.random.rand(30, 30)
>>> plt.imshow(image, cmap=plt.cm.hot)    
<matplotlib.image.AxesImage object at ...>
>>> plt.colorbar()    
<matplotlib.colorbar.Colorbar object at ...>

See also

More in the:

Основы индексирования и срезы

Существует много способов выбора подмножества данных или элементов
массива. Одномерные массивы — это просто, на первый взгляд они
аналогичны спискам Python:

In : arr = np.arange(10)

In : arr
Out: array()

In : arr
Out: 5

In : arr
Out: array()

In : arr = 12

In : arr
Out: array()

Как видно, если присвоить скалярное значение срезу, как например,
, значение присваивается всем элементам среза. Первым
важным отличием от списков Python заключается в том, что срезы массива
являются представлениями исходного массива. Это означает, что данные
не копируются и любые изменения в представлении будут отражены в
исходном массиве.

Рассмотрим пример. Сначала создадим срез массива :

In : arr_slice = arr

In : arr_slice
Out: array()

Теперь, если мы изменим значения в массиве , то они
отразятся в исходном массиве :

In : arr_slice = 12345

In : arr
Out: 
array()

«Голый» срез присвоит все значения в массиве:

In : arr_slice = 64

In : arr
Out: array()

Поскольку NumPy был разработан для работы с очень большими массивами,
вы можете представить себе проблемы с производительностью и памятью,
если NumPy будет настаивать на постоянном копировании данных.

Замечание

Если вы захотите скопировать срез в массив вместо отображения, нужно
явно скопировать массив, например, .

С массивами более высокой размерности существует больше вариантов. В
двумерных массивах каждый элемент это уже не скаляр, а одномерный
массив.

In : arr2d = np.array(, , ])

In : arr2d
Out: array()

Таким образом, к отдельному элементу можно получить доступ
рекурсивно, либо передать разделенный запятыми список
индексов. Например, следующие два примера эквивалентны:

In : arr2d
Out: array()

In : arr2d[]
Out: 3

Если в многомерном массиве опустить последние индексы, то возвращаемый
объект будет массивом меньшей размерности. Например, создадим массив
размерности \( 2 \times 2 \times 3 \):

In : arr3d = np.array(, ], , ]])

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

При этом — массив размерности \( 2 \times 3 \):

In : arr3d[]
Out: 
array(,
       ])

Можно присваивать как скаляр, так и массивы:

In : old_values = arr3d[].copy()

In : arr3d[] = 42

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

In : arr3d[] = old_values

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

Аналогично, возвращает все значения, чьи индексы
начинаются с , формируя одномерный массив:

In : arr3d
Out: array()

Это выражение такое же, как если бы мы проиндексировали в два этапа:

In : x = arr3d

In : x
Out: 
array(,
       ])

In : x[]
Out: array()

Индексирование с помощью срезов

Как одномерные объекты, такие как списки, можно получать срезы
массивов посредством знакомого синтаксиса:

In : arr
Out: array()

In : arr
Out: array()

Рассмотрим введенный выше двумерный массив . Получение срезов
этого массива немного отличается от одномерного:

In : arr2d
Out: 
array(,
       ,
       ])

In : arr2d
Out: 
array(,
       ])

Как видно, мы получили срез вдоль оси 0, первой оси. Срез, таким
образом, выбирает диапазон элементов вдоль оси. Выражение
можно прочитать как «выбираем первые две строки массива ».

Можно передавать несколько срезов:

In : arr2d
Out: 
array(,
       ])

При получении срезов мы получаем только отображения массивов того же
числа размерностей. Используя целые индексы и срезы, можно получить
срезы меньшей размерности:

In : arr2d
Out: array()

In : arr2d
Out: array()

Смотрите рис. .

Рисунок 1: Срезы двумерного массива

Линейная алгебра (numpy.linalg)¶

Модуль numpy.linalg содержит алгоритмы линейной алгебры, в частности нахождение определителя матрицы, решений
системы линейных уравнений, обращение матрицы, нахождение собственных чисел и собственных векторов матрицы,
разложение матрицы на множители: Холецкого, сингулярное, метод наименьших квадратов и т.д.

Команда	Описание
dot(a, b)	скалярное произведение массивов
vdot(a, b)	векторное произведение векторов
inner(a, b)	внутреннее произведение массивов
outer(a, b)	внешнее произведение векторов
tensordot(a, b)	тензорное скалярное произведение вдоль оси (размерность больше 1)
einsum(subscripts, *operands)	суммирование Эйншнейна Evaluates the Einstein summation convention on the operands.
linalg.matrix_power(M, n)	возведение квадратной матрицы в степень n
kron(a, b)	произведение Кронекера двух массивов
linalg.norm(a)	норма матрицы или вектора.
linalg.cond(a)	число обусловленности матрицы.
linalg.det(a)	определитель
linalg.slogdet(a)	знак и натуральный логарифм определителя
trace(a)	сумма элементов по диагонали.
linalg.cholesky(a)	разложение Холецкого
linalg.qr(a)	разложение QR
linalg.svd(a)	сингулярное разложение
linalg.solve(a, b)	решение линейного матричного уравнения или системы скалярных уравнений.
linalg.tensorsolve(a, b)	решение тензорного уравнения a x = b для x.
linalg.lstsq(a, b)	решение матричного уравнения методом наименьших квадратов
linalg.inv(a)	обратная матрица (для умножения)
linalg.pinv(a)	псевдо-обратная матрица (Мура-Пенроуза)
linalg.tensorinv(a)	«обратный» к многомерному массиву
linalg.eig(a)	собственные значения и правые собственные вектора квадратной
linalg.eigh(a)	собственные значения и собственные вектора эрмитовой или симметричной матрицы
linalg.eigvals(a)	собственные значения произвольной матрицы
linalg.eigvalsh(a)	собственные значения эрмитовой или действительной симметричной матрицы

Индексирование массивов

Когда ваши данные представлены с помощью массива NumPy, вы можете получить к ним доступ с помощью индексации.

Давайте рассмотрим несколько примеров доступа к данным с помощью индексации.

Одномерное индексирование

Как правило, индексирование работает так же, как вы ожидаете от своего опыта работы с другими языками программирования, такими как Java, C # и C ++.

Например, вы можете получить доступ к элементам с помощью оператора скобок [], указав индекс смещения нуля для значения, которое нужно получить.

При выполнении примера печатаются первое и последнее значения в массиве.

Задание целых чисел, слишком больших для границы массива, приведет к ошибке.

При выполнении примера выводится следующая ошибка:

Одно из ключевых отличий состоит в том, что вы можете использовать отрицательные индексы для извлечения значений, смещенных от конца массива.

Например, индекс -1 относится к последнему элементу в массиве. Индекс -2 возвращает второй последний элемент вплоть до -5 для первого элемента в текущем примере.

При выполнении примера печатаются последний и первый элементы в массиве.

Двумерное индексирование

Индексация двумерных данных аналогична индексации одномерных данных, за исключением того, что для разделения индекса для каждого измерения используется запятая.

Это отличается от языков на основе C, где для каждого измерения используется отдельный оператор скобок.

Например, мы можем получить доступ к первой строке и первому столбцу следующим образом:

При выполнении примера печатается первый элемент в наборе данных.

Если нас интересуют все элементы в первой строке, мы можем оставить индекс второго измерения пустым, например:

Это печатает первый ряд данных.

Массив NumPy

Как обсуждалось ранее, массив Numpy помогает нам в создании массивов. В этом разделе мы рассмотрим синтаксис и различные параметры, связанные с ним. Наряду с этим мы также рассмотрим некоторые примеры.

Синтаксис массива NumPy

(object)

Это общий синтаксис функции. Он имеет несколько параметров, связанных с ним, которые мы рассмотрим в следующем разделе.

Параметры

1. объект:array_like

Этот параметр представляет входной массив, который мы хотим получить в качестве выходного.

<2. тип:data-type

Этот параметр представляет тип данных, который будут иметь элементы массива. Это необязательный параметр. По умолчанию не указано, что он будет принимать минимальный тип, необходимый для хранения элементов.

3. порядок:

Это еще один необязательный параметр, который определяет расположение массива в памяти. Вновь созданный массив будет находиться в порядке c (row-major), если объект не является типом массива. Кроме того, если указано F, то есть (столбец-мажор), то он примет свою форму.

<4. admin:int

Этот необязательный параметр указывает максимальное количество измерений результирующего массива.

Возвращает

По завершении программы он возвращает массив заданного условия.

Примеры

На данный момент мы закончили охватывать все теории, связанные с массивом NumPy. Давайте теперь посмотрим несколько примеров и поймем, как это выполняется. После этого мы быстро перейдем к Normalize Numpy Array

import numpy as ppool.array(,
               )
print(a)

Выход:

Выше мы видим простой пример массива NumPy. Здесь мы сначала импортировали библиотеку NumPy. После чего мы использовали правильный синтаксис, а также указали тип, который должен быть float. В конце концов, наш результат оправдывает наш вклад и, следовательно, он проверяется. Точно так же вы можете сделать это и для сложного типа данных.

Numpy Процентиль против Квантиля

Percentile – Метод процентилей в модуле numpy, с помощью которого можно вычислить n-й процентиль заданных данных (элементов массива) вдоль заданной оси.

Numpy Quantile – Метод квантилей в модуле numpy, с помощью которого можно вычислить q-й квантиль заданных данных(элементов массива) вдоль заданной оси.

Давайте разберемся с помощью примера:

#numpy percentile vs numpy quantile

import numpy as np

arr = 

print("Array : ",arr)
print("\n")

print("25 percentile : ",np.percentile(arr, 25))
print("50 percentile : ",np.percentile(arr, 50))
print("75 percentile : ",np.percentile(arr, 75))
print("\n")

print(".25 Quantile : ",np.Quantile(arr, .25))
print(".50 Quantile : ",np.Quantile(arr, .50))
print(".75 Quantile : ",np.Quantile(arr, .75))

Выход:

Array :  


25 percentile :  20.0
50 percentile :  30.0
75 percentile :  40.0


.25 Quantile :  20.0
.50 Quantile :  30.0
.75 Quantile :  40.0

Объяснение:

Здесь, во-первых, мы импортировали модуль numpy как np. Во-вторых, мы взяли входной массив в переменной arr. В-третьих, мы применили функцию процентиля, в которой мы вычислили 25-й, 50-й и 75-й процентили и напечатали результат. В-четвертых, мы применили квантильную функцию, в которой мы вычислили 25-й, 50-й и 75-й процентили и напечатали результат. Следовательно, мы можем увидеть результат и узнать, что есть только разница, которая говорит 1 процентиль = .01 квантиль.

1D массив с использованием нулей Numpy()

Мы можем создавать одномерные массивы в Python со всеми его элементами, равными нулю ( ) используя этот метод. Давайте рассмотрим пример для лучшего понимания.

import numpy as np

arr1 = np.zeros(5)
print("The created array is: ",arr1) #generated array
print("It is of type:",type(arr1)) #type of array

Вывод :

Здесь, в приведенном выше коде,

• arr1 – это созданный новый массив. Как мы видим, мы только что прошли’ 5 ‘ к функции Numpy , без типа данных и порядка.
• По умолчанию значения и order рассматриваются как float и ‘ C ‘ соответственно. Это означает, что сгенерированный массив будет иметь элементы типа float и будет храниться в форме основной строки.
• Наконец, когда мы распечатываем массив, мы получаем массив 1D со всеми его плавающими элементами, имеющими значение . И тип() arr1 говорит нам, что он является членом класса .

Делать математику с NumPy

Любое руководство по NumPy не будет полным без числовых и математических операций, которые вы можете выполнять с NumPy! Давайте рассмотрим их:

добавит 1 к каждому элементу в массиве идобавит массив 2 к массиву 1. То же самое относится и к- все эти команды будут работать точно так же, как описано выше.

Вы также можете заставить NumPy возвращать различные значения из массива, например:

• вернет квадратный корень каждого элемента в массиве
• вернет синус каждого элемента в массиве
• вернет натуральный логарифм каждого элемента в массиве
• вернет абсолютное значение каждого элемента в массиве
• вернетсяесли массивы имеют одинаковые элементы и форму

Можно округлить разные значения в массиве:округляется до ближайшего целого числа,будет округляться до ближайшего целого числа ибудет округлять до ближайшего целого числа.

Массив нарезки

Все идет нормально; Создание и индексация массивов выглядит знакомо.

Теперь мы подошли к нарезке массивов, и это одна из функций, которая создает проблемы для начинающих массивов Python и NumPy.

Структуры, такие как списки и массивы NumPy, могут быть нарезаны. Это означает, что подпоследовательность структуры может быть проиндексирована и извлечена.

Это наиболее полезно при машинном обучении при указании входных и выходных переменных или разделении обучающих строк из строк тестирования.

Нарезка задается с помощью оператора двоеточия ‘:’ с ‘от’ а также ‘в‘Индекс до и после столбца соответственно. Срез начинается от индекса «от» и заканчивается на один элемент перед индексом «до».

Давайте рассмотрим несколько примеров.

Одномерная нарезка

Вы можете получить доступ ко всем данным в измерении массива, указав срез «:» без индексов.

При выполнении примера печатаются все элементы в массиве.

Первый элемент массива можно разрезать, указав фрагмент, который начинается с индекса 0 и заканчивается индексом 1 (один элемент перед индексом «до»)

Выполнение примера возвращает подмассив с первым элементом.

Мы также можем использовать отрицательные индексы в срезах. Например, мы можем нарезать последние два элемента в списке, начав срез с -2 (второй последний элемент) и не указав индекс «до»; это берет ломтик до конца измерения.

Выполнение примера возвращает подмассив только с двумя последними элементами.

Двумерная нарезка

Давайте рассмотрим два примера двумерного среза, которые вы, скорее всего, будете использовать в машинном обучении.

Разделение функций ввода и вывода

Распространено загруженные данные на входные переменные (X) и выходную переменную (y).

Мы можем сделать это, разрезая все строки и все столбцы до, но перед последним столбцом, затем отдельно индексируя последний столбец.

Для входных объектов мы можем выбрать все строки и все столбцы, кроме последнего, указав ‘:’ в индексе строк и: -1 в индексе столбцов.

Для выходного столбца мы можем снова выбрать все строки, используя ‘:’, и индексировать только последний столбец, указав индекс -1.

Собрав все это вместе, мы можем разделить 3-колоночный 2D-набор данных на входные и выходные данные следующим образом:

При выполнении примера печатаются разделенные элементы X и y

Обратите внимание, что X — это двумерный массив, а y — это одномерный массив

Сплит поезд и тестовые ряды

Обычно загруженный набор данных разбивают на отдельные наборы поездов и тестов.

Это разделение строк, где некоторая часть будет использоваться для обучения модели, а оставшаяся часть будет использоваться для оценки мастерства обученной модели.

Для этого потребуется разрезать все столбцы, указав «:» во втором индексе измерения. Набор обучающих данных будет содержать все строки от начала до точки разделения.

Тестовым набором данных будут все строки, начиная с точки разделения до конца измерения.

Собрав все это вместе, мы можем разделить набор данных в надуманной точке разделения 2.

При выполнении примера выбираются первые две строки для обучения и последняя строка для набора тестов.

Необычное индексирование

Необычное индексирование (fancy indexing) — это термин, принятый в
NumPy для описания индексации с использованием целочисленных
массивов.

Предположим, у нас есть массив размера \( 8 \times 4 \)

In : arr = np.empty((8, 4))

In : for i in range(8):
     ...:     arr = i

In : arr
Out: 
array(,
       ,
       ,
       ,
       ,
       ,
       ,
       ])

Чтобы выбрать подмножество строк в определенном порядке, можно
просто передать список или массив целых чисел, указывающих желаемый
порядок:

In : arr]
Out: 
array(,
       ,
       ,
       ])

Использование отрицательных индексов выделяет строки с конца:

In : arr]
Out: 
array(,
       ,
       ])

Передача нескольких индексных массивов делает кое-что другое:
выбирается одномерный массив элементов, соответствующий каждому
кортежу индексов:

In : arr = np.arange(32).reshape((8, 4))

In : arr
Out: 
array(,
       ,
       ,
       ,
       ,
       ,
       ,
       ])

In : arr, ]
Out: array()

Здесь выбраны элементы с индексами , , и
. Независимо от того какая размерность у массива (в нашем
случае двумерный массив), результат такого индексирования — всегда
одномерный массив.

Поведение индексирования в этом случае немного отличается
от того, что могли ожидать некоторые пользователи, а именно:
пользователь мог ожидать прямоугольную область, сформированную путем
выбора поднабора строк и столбцов матрицы. Ниже представлен один из
способов получения таких массивов с помощью необычного индексирования:

In : arr]]
Out: 
array(,
       ,
       ,
       ])

Имейте в виду, что необычное индексирование, в отличие от среза,
всегда копирует данные в новый массив.

1.4.1.1. What are NumPy and NumPy arrays?¶

NumPy arrays

Python objects:	high-level number objects: integers, floating point containers: lists (costless insertion and append), dictionaries (fast lookup)
NumPy provides:	extension package to Python for multi-dimensional arrays closer to hardware (efficiency) designed for scientific computation (convenience) Also known as array oriented computing

>>> import numpy as np
>>> a = np.array()
>>> a
array()

Tip

For example, An array containing:

• values of an experiment/simulation at discrete time steps
• signal recorded by a measurement device, e.g. sound wave
• pixels of an image, grey-level or colour
• 3-D data measured at different X-Y-Z positions, e.g. MRI scan
• …

Why it is useful: Memory-efficient container that provides fast numerical
operations.

In : L = range(1000)

In : %timeit i**2 for i in L
1000 loops, best of 3: 403 us per loop

In : a = np.arange(1000)

In : %timeit a**2
100000 loops, best of 3: 12.7 us per loop

NumPy Reference documentation

• On the web: https://numpy.org/doc/

• Interactive help:

  In : np.array?
  String Form:<built-in function array>
  Docstring:
  array(object, dtype=None, copy=True, order=None, subok=False, ndmin=0, ...
  

• Looking for something:

  >>> np.lookfor('create array') 
  Search results for 'create array'
  ---------------------------------
  numpy.array
      Create an array.
  numpy.memmap
      Create a memory-map to an array stored in a *binary* file on disk.
  

  In : np.con*?
  np.concatenate
  np.conj
  np.conjugate
  np.convolve
  

Примеры для разных размеров шага

Пример 1: Для натурального не комплексного числа –

import numpy as np.mgrid
print(a)

Выход:

array(,
        ,
        ,
        ],

       ,
        ,
        ,
        ]])

Пример 2: Для комплексного числа –

import numpy as np.mgrid
print(a)

Выход:

array()

Объяснение:

На приведенных выше примерах мы видим, как функция Numpy mgrid() используется для получения ndarrays. “Массивы” имеют одно и то же измерение. Стоп – значение не является включающим. Если длина шага не является комплексным числом. Однако если длина шага является комплексным числом (например, 4j). Затем интерпретируется целая часть его величины. И количество точек, которые нужно создать между началом и остановкой. В этом случае стоп-значение является включительным.

Перестройка массива

После нарезки данных вам может понадобиться изменить их.

Например, некоторые библиотеки, такие как scikit-learn, могут требовать, чтобы одномерный массив выходных переменных (y) был сформирован как двумерный массив с одним столбцом и результатами для каждого столбца.

Некоторые алгоритмы, такие как рекуррентная нейронная сеть с короткой кратковременной памятью в Keras, требуют ввода данных в виде трехмерного массива, состоящего из выборок, временных шагов и функций.

Важно знать, как изменить ваши массивы NumPy, чтобы ваши данные соответствовали ожиданиям конкретных библиотек Python. Мы рассмотрим эти два примера

Форма данных

Массивы NumPy имеют атрибут shape, который возвращает кортеж длины каждого измерения массива.

Например:

При выполнении примера печатается кортеж для одного измерения.

Кортеж с двумя длинами возвращается для двумерного массива.

Выполнение примера возвращает кортеж с количеством строк и столбцов.

Вы можете использовать размер измерений вашего массива в измерении формы, например, указав параметры.

К элементам кортежа можно обращаться точно так же, как к массиву, с 0-м индексом для числа строк и 1-м индексом для количества столбцов. Например:

Запуск примера позволяет получить доступ к конкретному размеру каждого измерения.

Изменить форму 1D в 2D Array

Обычно требуется преобразовать одномерный массив в двумерный массив с одним столбцом и несколькими массивами.

NumPy предоставляет функцию reshape () для объекта массива NumPy, который можно использовать для изменения формы данных.

Функция reshape () принимает единственный аргумент, который задает новую форму массива. В случае преобразования одномерного массива в двумерный массив с одним столбцом кортеж будет иметь форму массива в качестве первого измерения (data.shape ) и 1 для второго измерения.

Собрав все это вместе, мы получим следующий проработанный пример.

При выполнении примера печатается форма одномерного массива, изменяется массив, чтобы иметь 5 строк с 1 столбцом, а затем печатается эта новая форма.

Изменить форму 2D в 3D Array

Обычно требуется преобразовать двумерные данные, где каждая строка представляет последовательность в трехмерный массив для алгоритмов, которые ожидают множество выборок за один или несколько временных шагов и одну или несколько функций.

Хорошим примером являетсямодель в библиотеке глубокого обучения Keras.

Функция изменения формы может использоваться напрямую, указывая новую размерность. Это ясно с примером, где каждая последовательность имеет несколько временных шагов с одним наблюдением (функцией) на каждый временной шаг.

Мы можем использовать размеры в атрибуте shape в массиве, чтобы указать количество выборок (строк) и столбцов (временных шагов) и зафиксировать количество объектов в 1

Собрав все это вместе, мы получим следующий проработанный пример.

При выполнении примера сначала печатается размер каждого измерения в двумерном массиве, изменяется форма массива, а затем суммируется форма нового трехмерного массива.

Индексирование и нарезка

Индексирование и нарезка массивов NumPy работает очень похоже на работу со списками Python:вернет элемент в 5-м индексе, ивернет элемент в index . Вы также можете выбрать первые пять элементов, например, с помощью двоеточия (:).вернет первые пять элементов (индекс 0–4) ивернет первые пять элементов в столбце 4. Вы можете использоватьполучить элементы от начала до индекса 2 (не включая индекс 2) иливернуться со 2-го индекса до конца массива.вернет элементы с индексом 1 во всех строках

Присвоение значений массиву NumPy, опять же, очень похоже на это в списках Python:присвоит значение 4 элементу с индексом 1; Вы можете сделать это для нескольких значений:или используйте нарезку при назначении значений:изменит весь 11-й столбец на значение 10.

Различные методы нормализации массива NumPy

1. Нормализация с помощью NumPy Sum

В этом методе мы используем NumPy ndarray sum для вычисления суммы каждой отдельной строки массива. После чего мы делим элементы массива if на сумму. Давайте рассмотрим это на примере.

import numpy as ppool.array(,
               )
print(a))
print(b)/b
print(c)

Выход:

Это еще один способ нормализации массива. Этот метод действительно эффективен для нормализации по строкам.

2. Нормализация с помощью sklearn

Sklearn-это модуль python, широко используемый в науке о данных и интеллектуальном анализе. Используя это href=”https://en.wikipedia.org/wiki/Method”>метод также мы можем нормализовать массив. Это следует очень простой процедуре, и давайте разберемся в ней на примере. href=”https://en.wikipedia.org/wiki/Method”>метод также мы можем нормализовать массив. Это следует очень простой процедуре, и давайте разберемся в ней на примере.

from sklearn import preprocessing
print(preprocessing.normalize(, ]))

Выход:

3. Нормализация с помощью понимания списка

Вы также можете нормализовать список в python. Понимание списка, как правило, предлагает более короткий синтаксис, который помогает в создании нового списка из существующего списка. Давайте рассмотрим это на примере.

list = ]
norm_list = [i / sum(j) for j in list for i in j]
print(norm_list)

Посмотрите, как нам удалось нормализовать наш существующий список. Здесь мы видим, что мы разделили каждый элемент в списке на сумму всех элементов. Это тоже хороший вариант для нормализации.

4. Нормализация с использованием цикла For

Мы также продвигаем процесс нормализации с помощью цикла for. Используя цикл for, мы можем вычислить сумму всех элементов. Затем разделите каждый элемент на эту сумму. Здесь я советую вам использовать массив NumPy. Продолжая деление, вы можете получить ошибку, так как “list/int” не является подходящим типом данных.

import numpy as ppool
def _sum(arr):  
      
   
      
    for i in arr: 
        + i 
          
    return(sum)  
  .array( ) (arr)  (arr)  
print (ans) /ans
print(b)

Выход:

Можем Ли Мы Найти Разницу Между Двумя Массивами Numpy С Разными Формами?

Простыми словами, Нет, мы не можем найти различия или использовать функцию вычитания numpy в двух массивах numpy, которые имеют разные формы.

Давайте рассмотрим это на одном примере,

import numpy as np
a1 = , ]
a2 = , ]

print ("1st Input array : ", a1) 
print ("2nd Input array : ", a2) 
	.subtract(a1, a2) 
print ("Difference of two input arrays : ", dif)

Выход:

Объяснение

Если форма двух массивов numpy будет отличаться, то мы получим valueerror. Ошибка значения будет говорить что – то вроде, например.

ValueError: operands could not be broadcast together with shapes (2,3) (2,)

Здесь, в этом примере, мы получаем valueerror, потому что входной массив a2 имеет другую форму, чем входной массив a1. Чтобы получить разницу без какой-либо ошибки значения, обязательно проверьте форму массивов.

Использование функции reshape()

Первым делом, прежде чем попрактиковаться в использовании данной функции, вам следует импортировать библиотеку NumPy. После этого можно приступать к работе.

Далее мы покажем различные варианты использования функции .

Пример 1: преобразование одномерного массива в двумерный

Итак, давайте разберем, как с помощью функции преобразовать одномерный массив в двумерный.

В этом сценарии для создания одномерного массива из 10 элементов используется функция .

Первая функция используется для преобразования одномерного массива в двумерный, состоящий из 2 строк и 5 столбцов. Здесь функция вызывается с использованием имени модуля .

А вторая функция используется для преобразования одномерного массива в двумерный, состоящий из 5 строк и 2 столбцов. Здесь уже функция вызывается с использованием массива NumPy с именем .

import numpy as np

np_array = np.arange(10)
print("Исходный массив : \n", np_array)

new_array = np.reshape(np_array, (2, 5))
print("\n Измененный массив с 2 строками и 5 столбцами : \n", new_array)

new_array = np_array.reshape(5, 2)
print("\n Измененный массив с 5 строками и 2 столбцами : \n", new_array)

Если вы запустите описанную выше программу, то получите результат, как на следующем скриншоте. Первый показывает исходный массив, а второй и третий выводят преобразованные массивы.

Пример 2: преобразование одномерного массива в трехмерный

Теперь давайте посмотрим, как при помощи функции преобразовать одномерный массив в трехмерный.

Воспользуемся функцией для создания одномерного массива из 12 элементов.

Функция преобразует созданный одномерный массив в трехмерный размером 2х2х3. Здесь функция вызывается с использованием NumPy-массива .

import numpy as np

np_array = np.array()
print("Исходный массив : \n", np_array)

new_array = np_array.reshape(2, 2, 3)
print("\n Преобразованный 3D массив : \n", new_array)

Выполнив данный код, вы получите следующий вывод. Как и в прошлый раз, первый показывает изначальный массив, второй – преобразованный массив.

Пример 3: изменение формы массива NumPy с учетом порядка

Как вы помните, у функции есть третий — опциональный — аргумент, задающий порядок индексации. Давайте посмотрим, как он применяется на практике.

Как и в первом примере, воспользуемся функцией для создания одномерного массива из 15 элементов.

Первая функция используется для создания двумерного массива из 3 строк и 5 столбцов с упорядочением в стиле C. В то время как вторая функция используется для создания двумерного массива из 3 строк и 5 столбцов с упорядочением в стиле Фортрана.

import numpy as np

np_array = np.arange(15)
print("Исходный массив : \n", np_array)

new_array1 = np.reshape(np_array, (3, 5), order='C')
print("\n Преобразованный 2D массив, упорядоченный в стиле С : \n", new_array1)

new_array2 = np.reshape(np_array, (3, 5), order='F')
print("\n Преобразованный 2D массив, упорядоченный в стиле Фортрана : \n", new_array2)

Давайте выполним наш код. Вот, что мы получим. Как и раньше, первый показывает исходный массив значений. Второй показывает значения массива, упорядоченного по строкам. Третий – упорядоченного по столбцам.

Синтаксис

Формат:

array = numpy.arange(start, stop, step, dtype=None)

Где:

• start -> Начальная точка (включенная) диапазона, которая по умолчанию установлена на 0;
• stop -> Конечная точка (исключенная) диапазона;
• step -> Размер шага последовательности, который по умолчанию равен 1. Это может быть любое действительное число, кроме нуля;
• dtype -> Тип выходного массива. Если dtype не указан (или указан, как None), тип данных будет выведен из типа других входных аргументов.

Давайте рассмотрим простой пример, чтобы понять это:

import numpy as np
 
a = np.arange(0.02, 2, 0.1, None)
 
print('Linear Sequence from 0.02 to 2:', a)
print('Length:', len(a))

Это сгенерирует линейную последовательность от 0,2 (включительно) до 2 (исключено) с размером шага 0,1, поэтому в последовательности будет (2 — 0,2) / 0,1 — 1 = 20 элементов, что является длиной результирующего массив numpy.

Вывод:

Linear Sequence from 0.02 to 2: 
Length: 20

Вот еще одна строка кода, которая генерирует числа от 0 до 9 с помощью arange(), используя размер шага по умолчанию 1:

>>> np.arange(0, 10)
array()

Если размер шага равен 0, это недопустимая последовательность, поскольку шаг 0 означает, что вы делите диапазон на 0, что вызовет исключение ZeroDivisionError Exception.

import numpy as np

# Invalid Step Size!
a = np.arange(0, 10, 0)

Вывод:

ZeroDivisionError: division by zero

ПРИМЕЧАНИЕ. Эта функция немного отличается от numpy.linspace(), которая по умолчанию включает как начальную, так и конечную точки для вычисления последовательности. Он также не принимает в качестве аргумента размер шага, а принимает только количество элементов в последовательности.

Что такое Стандартное отклонение Numpy?

Numpy – это инструментарий, который помогает нам в работе с числовыми данными. Он содержит набор инструментов для создания структуры данных, называемой массивом Numpy. Это в основном сетка строк и столбцов чисел.

Стандартное отклонение-это статистика, которая измеряет величину вариации в наборе данных относительно его среднего значения и вычисляется как квадратный корень дисперсии. Он рассчитывается путем определения отклонения каждой точки данных относительно среднего.

Где,

• Отклонение SD
• x значение массива
• ты имеешь в виду
• N значений

Модуль numpy в python предоставляет различные функции, одной из которых является numpy.std(). Он используется для вычисления стандартного отклонения вдоль указанной оси. Эта функция возвращает стандартное отклонение элементов массива numpy. Квадратный корень среднего квадратного отклонения (известного как дисперсия) называется стандартным отклонением.

Standard Deviation = sqrt(mean(abs(x-x.mean( ))**2

Дискретное преобразование Фурье (numpy.fft)¶

Прямое преобразование	Обратное преобразование	Описание
fft(a)	ifft(a)	одномерное дискретное преобразование Фурье
fft2(a)	ifft2(a)	двумерное дискретное преобразование Фурье
fftn(a)	ifftn(a)	многомерное дискретное преобразование Фурье
rfft(a)	irfft(a)	одномерное дискретное преобразование Фурье (действительные числа)
rfft2(a)	irfft2(a)	двумерное дискретное преобразование Фурье (действительные числа)
rfftn(a)	irfftn(a)	многомерное дискретное преобразование Фурье (действительные числа)
hfft(a)	ihfft(a)	преобразование Фурье сигнала с Эрмитовым спектром
fftfreq(n)		частоты дискретного преобразования Фурье
fftshift(a)	ifftshift(a)	преобразование Фурье со сдвигом нулевой компоненты в центр спектра

Арифметические операции над массивами NumPy

Создадим два массива NumPy и продемонстрируем выгоду их использования.

Массивы будут называться и :

При сложении массивов складываются значения каждого ряда. Это сделать очень просто, достаточно написать :

Новичкам может прийтись по душе тот факт, что использование абстракций подобного рода не требует написания циклов for с вычислениями. Это отличная абстракция, которая позволяет оценить поставленную задачу на более высоком уровне.

Помимо сложения, здесь также можно выполнить следующие простые арифметические операции:

Довольно часто требуется выполнить какую-то арифметическую операцию между массивом и простым числом. Ее также можно назвать операцией между вектором и скалярной величиной. К примеру, предположим, в массиве указано расстояние в милях, и его нужно перевести в километры. Для этого нужно выполнить операцию :

Как можно увидеть в примере выше, NumPy сам понял, что умножить на указанное число нужно каждый элемент массива. Данный концепт называется трансляцией, или broadcating. Трансляция бывает весьма полезна.