Пример построения сетевого графика

Временные параметры сетей. Резервы времени.

Основными
временными параметрами сетей являются
ранние и поздние сроки наступления
(совершения) событий. Зная их, можно
вычислить остальные параметры сети –
сроки начала и окончания работ и резервы
времени событий и работ.

Обозначим
–
продолжительность работы с начальным
событиемi

и конечным событием j
.

Ранний
срок


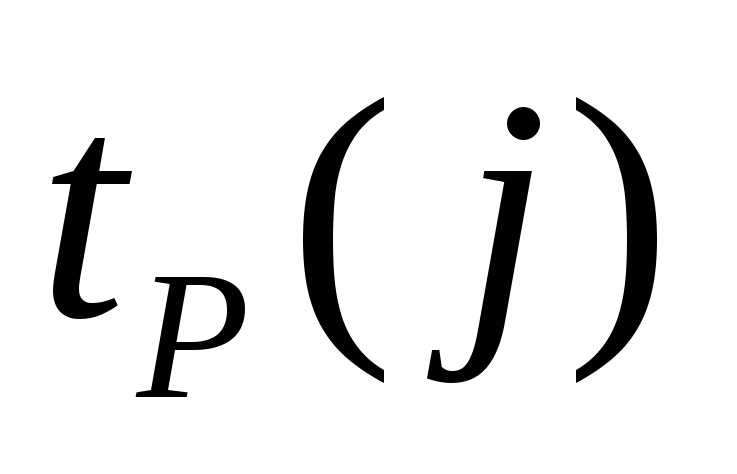совершения событияj

определяется величиной наиболее
длительного отрезка пути от исходного
до рассматриваемого события, причем
,
агдеN
— номер
завершающего события. Правило вычисления:

где
максимум берется по всем событиям i
, непосредственно
предшествующим событию j

(соединены стрелками).

Поздний
срок


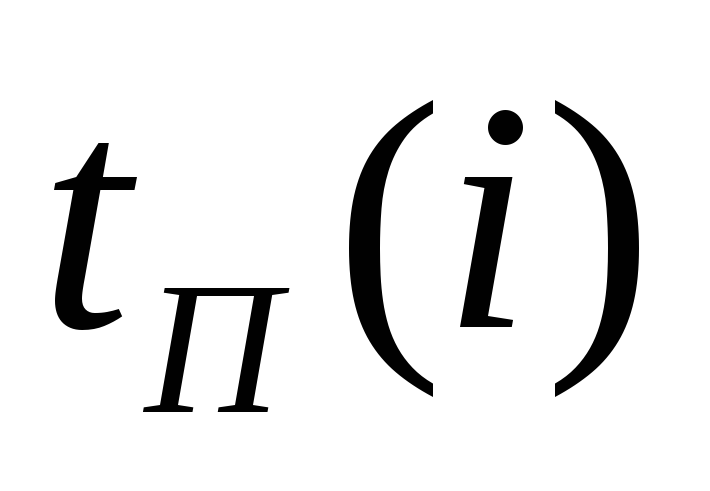свершения
событияi
характеризует
самый поздний допустимый срок, к которому
должно совершится событие, не вызывая
при этом срыва срока совершения конечного
события. Правило вычисления:

где
минимум берется по всем событиям j
,
непосредственно следующим за событиемi
.

Поздние
сроки событий определяются «обратным
ходом», начиная с завершающего события,
с учетом соотношения
,
т. е. поздний и ранний сроки совершения
завершающего события равны между собой.

Резерв


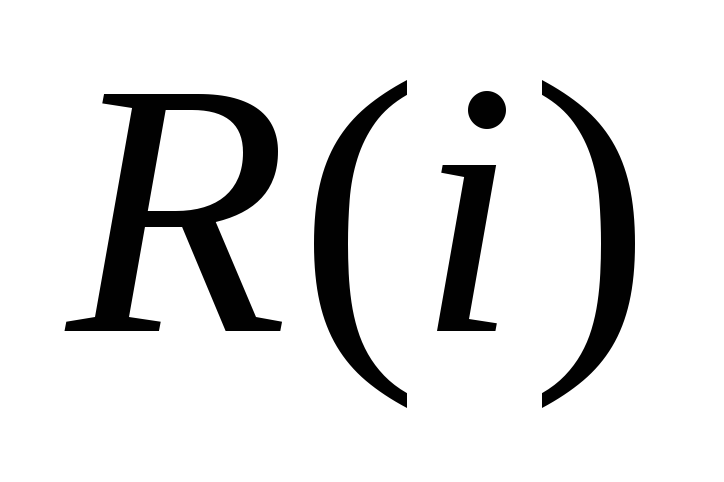событияi
показывает,
на какой предельно допустимый срок
может задержаться свершение событияi

без нарушения срока наступления
завершающего события:

.

События
лежащие на критическом пути (критические
события) резервов не имеют.

Существуют
различные методы расчета параметров
сети: табличный и графический.

Рассмотрим
графический метод.

При
расчетах сетевого графика каждый круг,
изображающий событие, делим диаметрами
на четыре сектора:

Пример 55. Рассмотрим
сеть проекта, представленную следующим
графиком.

На
графике события представлены кругами,
а работы стрелками. Робота может
обозначаться как буквой, надписанной
на графике рядом с соответствующей
работе стрелкой, либо через номера
событий из которых начинается и
заканчивается работа.

Найти
критический путь. Сколько времени
потребуется для завершения проекта?
Можно ли отложить выполнение роботы D

без отсрочки завершения проекта в целом?
Насколько недель можно отложить
выполнение работы C

без отсрочки завершения проекта в целом?

1
этап. При вычислении раннего срока
свершения события
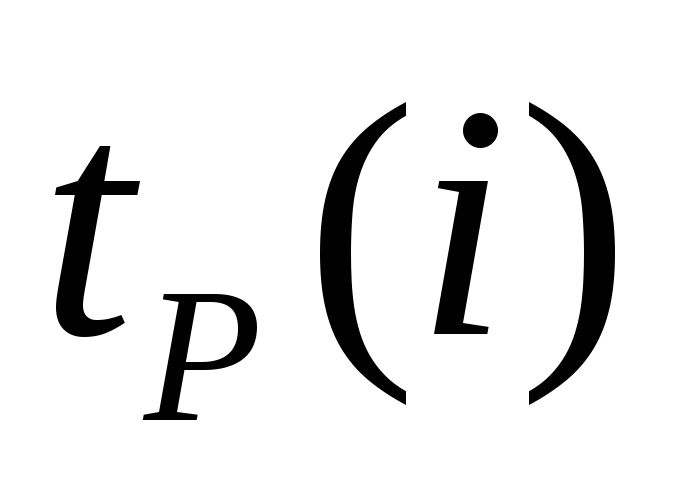перемещаемся
от исходного события 1 завершающему
событию 6.

.

В
событие 2 входит только одна работа:
.

Аналогично
.

В
событие 4 входят две работы →

Отсюда следует,
что критическое время выполнения проекта
= 22.

Внесем соответствующие
данные в сетевой график.

2
этап. При вычислении позднего
срока
t
п
(i
) свершения события
I

перемещаемся от завершающего события
6 к исходному событию 1 по сетевому
графику против направления стрелок.

.

Из
события 4 выходят две работы: (4, 5) и (4,
6). Поэтому определяем поздний срок
наступления события t
п
( 4)
по каждой
из этих работ:

Внесем полученные
данные в сетевой график.

3
этап. Вычисляем резерв

событияi
, то есть из
чисел, полученных на этапе 2, вычитаем
числа, полученные на этапе 1.

4
этап. У критических событий резерв
времени равен нулю, так как ранние и
поздние сроки их свершения совпадают.
Критические события 1, 2, 4, 5, 6 и определяют
критический путь 1-2-4-5-6, который по
определению должен быть самым
продолжительным по времени. На сетевом
графике мы его покажем двумя чертами.

Теперь можно
ответить на вопросы задачи.

Для
завершения проекта потребуется 22 недели.
Работа D

расположена на критическом пути. Поэтому
ее нельзя отложить без отсрочки завершения
проекта в целом. Работа C

не расположена на критическом пути, ее
можно задержать на
(недели).

Метод сетевой модели номер два

Вторым методом сетевого планирования, по праву завоевавшим популярность среди проект-менеджеров, является диаграмма, называемая «вершина – работа». В англоязычной версии модель сокращенно обозначается как AoN (Activity on Node). Метод отличается большей простой и наглядностью, предлагает узлами модели делать не события, а работы. При этом длина прямоугольников, обозначающих операции, может указывать на их длительность во времени. Отношения предшествования между ними оформляются прямыми или фигурными стрелками.

Такую диаграмму сформировать значительно проще, чем AoA. Тем не менее, алгоритм работы над ней очень похож. События на диаграмме не размещаются, но они предполагаются в завершении каждой работы. Помимо прочего, событиям все-таки уготовано место на сетевом графике, но в форме особых фактов, именуемых вехами. Веха – это особенное значимое событие проекта, и не каждая операция должна ею завершаться. Поэтому диаграмма может быть разгружена от несущественных событий, но отражать важные, ключевые моменты проектной реализации.

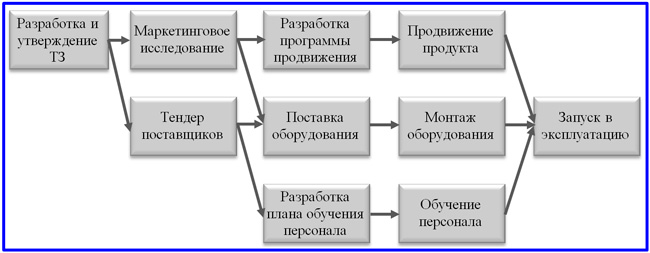Пример сетевой диаграммы метода «вершина – работа»

Если воспользоваться возможностью вариации длины прямоугольников работ, превращая их в ленты, размер которых соответствует длительности реализации, то сетевой график превращается в диаграмму Ганта. Диаграмма вида AoN при этом становится похожей на АоА. В методе AoN отпадает необходимость в изображении фиктивных работ, требуемых в модели «ребро – работа» для своеобразной «упаковки» событий. Благодаря этому лишние, искусственные сущности исключаются из поля зрения менеджера проекта. Вехи в этом отношении являются более интересным решением, располагаясь, как и все работы, в узлах сетевого графика.

Работы перестают выполнять двойную функцию связующих события элементов и непосредственного обозначения выполняемых операций. Для метода AoN не требуется нумерации, что дает PM мобильность для свободного маневрирования числом мероприятий. И в этом кроется еще одно удобство метода «вершина – работа». В сетевой диаграмме должны быть учтены возможности применения различных связей предшествования. Их количество не столь велико, как может показаться на первый взгляд. Оно связано с вариантом связи предшествования и с эффектом отставания или опережения в отношении к примененной типовой связи. Все это мы рассмотрим в отдельном материале, посвященном практике сетевого планирования и управления.

В настоящей статье мы рассмотрели методы сетевого планирования и управления. В современной проектной практике отдается предпочтение методу AoN как более доступному и наглядному. Это не означает, что метод АоА плох, многие специалисты, освоив его, с успехом применяют. Обе модели приводят к одному и тому же результату, но с двух взаимосвязанных сторон: работ и событий. Проект-менеджер должен понимать суть и уметь применять каждый из представленных инструментов. Это связано с тем, что задача сетевого планирования состоит в поиске наиболее экономичных, ясных решений построения событийной и временной последовательности в условиях ограничений.

Автоматическая сетевая диаграмма проекта с критическим путем в EXCEL

Построим автоматическую сетевую диаграмму проекта. Сетевую диаграмму изобразим на диаграмме MS EXCEL типа Точечная. На этой диаграмме выведем работы проекта в виде точек, стрелками изобразим связи между работами. Также изобразим на диаграмме критический(ие) путь(и). Сетевая диаграмма будет автоматически перестраиваться при изменении связей между работами и их длительности.

Данная статья является третьей статьей в цикле статей посвященных построению сетевой диаграммы проекта и является синтезом первых двух:

1. В статье Метод критического пути в MS EXCEL показано как рассчитать длительность проекта, определить работы на критическом пути и как построить сетевую диаграмму проекта на листе MS EXCEL. Основной недостаток – при изменении связей между работами пользователю потребуется вносить серьезное изменение в сетевую диаграмму.
2. В статье Автоматическая сетевая диаграмма проекта в MS EXCEL показано, как имея перечень работ и связи между ними, вычислить все пути проекта и отобразить их на стандартной диаграмме типа Точечная. При изменении связей – пути автоматически пересчитываются. Однако, критический путь не вычислялся в этой статье.

Рекомендуется прочитать вышеуказанные статьи перед первым прочтением.

Ниже показана диаграмма, которую мы будем создавать в этой статье. На диаграмме отображены все работы проекта (от А до U, синие точки), связи между ними (стрелки), работы на критическом пути (красные точки), критический путь (красные стрелки).

Примечание : Слово диаграмма используется в 2-х смыслах: сетевая диаграмма проекта (стандартный термин из управления проектом, Activity-on-node diagram ) и диаграмма MS EXCEL ( Excel Chart , см. вкладку , группа ). Диаграмма MS EXCEL типа Точечная будет использоваться для построения сетевой диаграммы проекта.

При изменении связей между работами и/или их длительности происходит перерасчет критического пути и сетевая диаграмма автоматически обновляется. Например, значительное увеличение длительности работы М (в нижнем пути сетевой диаграммы) приведет к изменению критического пути.

Такая сетевая диаграмма отображает критический путь даже нагляднее, чем стандартная диаграмма Ганта , хотя, конечно, не заменяет ее.

ВНИМАНИЕ! Построение данной сетевой диаграммы в этой статье приведено лишь с целью демонстрации технической реализуемости такого построения в MS EXCEL. Не ставилось целью сделать “удобную программу для пользователей”

Это означает, что при изменении пользователем количества работ/ добавления связей между работами (например, использования более 5 последователей), переименовании листов, рядов диаграммы и других изменений, в файле примера может потребоваться дополнительная настройка формул.

Такая настройка потребует от пользователя серьезных знаний MS EXCEL и времени.

Исходная информация

В качестве исходной информации дан перечень работ, их длительность и связи между работами.

Также вручную задаются координаты для отображения на диаграмме работ (диапазон ВА12:ВВ34 ).

Другой информации для построения сетевой диаграммы и вычисления критического пути не требуется.

Вычисление путей сетевой диаграммы

Как и в статье Автоматическая сетевая диаграмма проекта в MS EXCEL начнем построение сетевой диаграммы с вычисления путей.

В отличие от указанной статьи, здесь увеличено количество рассчитываемых путей (до 15) и максимальная длина путей (до 10 работ, включая вехи начала и окончания).

Алгоритм вычисления путей аналогичен, однако формулы изменены, чтобы позволить пользователю быстро увеличивать количество путей проекта и их длину.

Начиная с шага №1 (начиная со строки 96) формулы можно копировать вниз и вправо, чтобы при необходимости увеличить количество путей и их длину (количество шагов). На каждом шаге длина путей увеличиваются на одну работу. В случае наличия нескольких последователей у работы – увеличивается количество возможных путей.

После вычисления всех шагов, в диапазоне R62:AA76 выводится перечень всех путей проекта, содержащие входящие в них работы.

Построение сетевой диаграммы

Сначала на диаграмме выводятся работы (синие точки, ряд Работы ).

Затем выводятся все возможные пути проекта (ряды Путь_1, Путь_2, …, Путь_15 ).

Все работы, находящиеся на критическом пути, отмечаются красным цветом. Также на диаграмму выводится критический путь. Если путей несколько, то выводятся все пути (в файле примера выводятся максимум 3 критических пути). Если длительность работы О увеличить до 8 дней, то 3 пути станут критическими с длительностью по 65 дней.

Одновременно, работы проекта отображаются на диаграмме Ганта.

Построение сетевого графика

В нашем примере для построения сетевого графика необходимо составить формуляр операций, его можно использовать в качестве образца на практике.

В таблицу сведем следующие данные по каждой операции:

• номер операции;
• предшествующие операции;
• количество исполнителей;
• продолжительность операции в днях.

В таблице операций их номера соответствует нумерации в карточке-определителе в соответствии с группировкой параллельных операций.

На основе таблицы операций и карточки-определителя с учетом произведенной группировки параллельных операций осуществляется построение сетевого графика.

Сетевой график, пример

Определим критический путь. Критический путь на данном сетевом графике составляют операции: 1, 4, 5, 7, 8, 9, 13, 15, 16, 17, 18, 19, 24, 25, 28, 29, 31, 32, 33 (34), 35.

В результате построения сетевого графика работы можно сделать вывод, что деятельность организации не укладывается в заданный срок равный 22 рабочим дням, составляя вместо этого 26 дней. При этом операции первой, второй и третьей недели не укладываются в заданный для них срок, равный 5 рабочим дням. По сетевой модели операции 1 недели длятся 7 дней, 2 недели – 6 дней, 3 недели – 6 дней. Операции четвертой и пятой недель укладываются в заданные для них сроки.

Для соблюдения запланированных сроков произведем корректировку сетевого графика.

В нашем примере сетевого графика по данным карточки-распределителя можно сделать вывод, что для некоторых операций в рамках запланированных действий существует резерв специалистов в отделе. Учитывая, что общая численность сотрудников относительно невелика, можно воспользоваться способом корректировки сетевой модели с привлечением дополнительных ресурсов, в качестве которых выступают свободные на момент реализации операции специалисты данного отдела. Благодаря этому сократится срок выполнения операций критического пути, соответственно и сроки всей сетевой модели. Корректировке подлежат операции 1, 2 и 3 недель, так как операции 4 и 5 недель сетевого графика укладываются в заданные сроки.

После корректировки осуществим построение альтернативного сетевого графика.

Необходимо привлечь дополнительных специалистов для выполнения операций 4 (отдел специальных программ), 13 (отдел по организации оздоровительной кампании) и 18 (отдел специальных программ). Расчет трудоемкости операций (Q) определим исходя из произведения числа специалистов (N), выполняющих операцию, на число дней (t), выделенных для ее выполнения:

Q = N * t

Q4 = 2*4 = 8 ч/дн

Q13 = 2*3 = 6 ч/дн

Q18 = 2*2 = 4 ч/дн

В отделе специальных программ работает 5 человек, но в выполнении операции 4 задействовано только 2 человека. В результате привлечения двух специалистов новый срок выполнения операции составит: 8 / 4 = 2 дня. Следовательно, операция 4 будет выполняться 2 дня вместо 4 дней.

В отделе по организации оздоровительной кампании работает 3 специалиста, но в выполнении операции 13 занято только два человека. В данном случае привлечение одного дополнительного специалиста позволит сократить срок выполнения операции: 6 / 3 = 2 дня. Следовательно, операция 13 будет выполняться 2 дня вместо 3 дней.

В выполнении операции 18 задействовано 2 специалиста отдела специальных программ. Привлечение двух дополнительных специалистов позволит сократить срок ее выполнения: 4 / 4 = 1 день. Следовательно, операция 18 будет выполняться 1 день вместо 2 дней.

В результате получаем срок выполнения операций после корректировки сетевого графика с привлечением дополнительных ресурсов:

26 – 2 – 1 – 1 = 22 дня.

Таким образом, за счет произведенной коррекции сетевого графика срок выполнения операций, соответствует изначально заданному сроку в 22 рабочих дня.

Альтернативный график будет аналогичен предыдущему в плане своей структуры, корректировке подвергнуты сроки реализации операций согласно построенной сетевой модели.

Альтернативный сетевой график

Алгоритм построения сетевого графика

Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.

Шаг 1. Определить основную цель проекта

Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.

Шаг 2. Выявить ограничения

Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.

Шаг 4. Оценить длительность работ

Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.

Шаг 5. Определить последовательность работ

Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.

Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.

Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.

Шаг 6. Указать связи между работами

Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.

Шаг 7. Определить раннее начало и раннее окончание

Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.

Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.

Шаг 8. Определить поздние начало и окончание

Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.

Шаг 9. Определить временной резерв

Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.

Шаг 10. Выявить критический путь

Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.

Исходные данные

Руководство рекламного агентства приняло решение о выходе в свет нового рекламного продукта для своих клиентов. Перед сотрудниками фирмы были поставлены такие задачи: рассмотреть идеи рекламных брошюр, привести аргументы в пользу того или иного варианта, создать макет, подготовить проект договора для клиентов и послать всю информацию руководству на рассмотрение. Для информирования клиентов необходимо провести рассылку, расклеить плакаты и обзвонить все фирмы, имеющиеся в базе данных.

Кроме этого, главный руководитель составил детальный план всех необходимых действий, назначил ответственных сотрудников и определил время.

Начнем построение сетевого графика. Пример имеет данные, представленные на следующем рисунке:

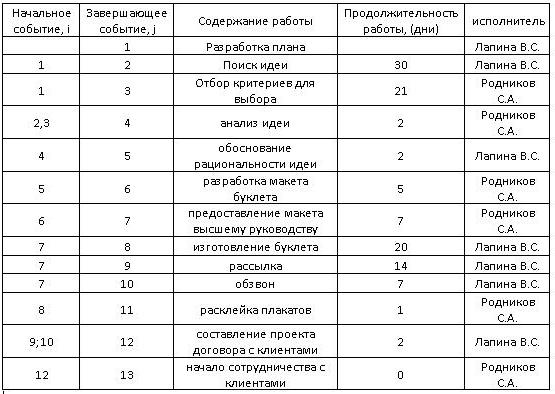
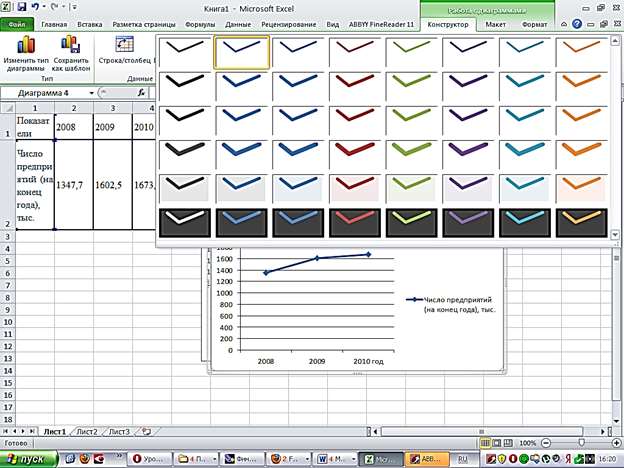
Работа с Excel 2010 года

Построение графиков и диаграмм в Excel 2010 идет по тому же принципу, что и в предыдущей версии. Однако есть и некоторые различия, которыми пользователь должен владеть. Так, при построении графиков можно воспользоваться вкладкой «Работа с диаграммами», в которой полезным будет Конструктор, где многочисленные стили оформления собраны в одном поле и выбираются двумя кликами.

Вкладки «Макет» и «Формат» позволяют привести к желаемому виду все элементы картинки, добавить к диаграмме название и прорисовать сетку координат, изменить наклон осей. Эти функции помогают и при работе с объемными рисунками.

Варианты связей и отношение предшествования

Сетевые методы планирования строятся по моделям, в которых проект представляется как целостная совокупность взаимосвязанных работ. Данные модели во многом формируются типом и видом связей между операциями реализации проекта. С позиции типа различаются жесткие, мягкие и ресурсные связи. Видовое различие взаимосвязанности операций основано на отношения предшествования. Рассмотрим основные типы связи.

Мягкие связи. Им соответствует особая, «дискреционная» логика, дающая «мягкую» основу для выбора операций к размещению на диаграмму, диктуемого технологией. В то время как технология длительный период развивалась на протяжении многих циклов, вырабатываются правила делового оборота, не требующие дополнительной фиксации и планирования. Это экономит время, место модели, стоимость и не требует дополнительного контроля со стороны PM. Поэтому менеджер проекта сам решает, нужна ему такая выделенная операция, или нет.
Жесткие связи. Данный вид связей основан на технологической логике. Они предписывают выполнение конкретных действий строго после других, что сообразно с процессуальной логикой. Например, наладку оборудования можно осуществлять только после его монтажа. Тестирование недочетов технологии допустимо проводить, если сдача ее в опытную эксплуатацию произошла и т.д

Иными словами, принятая технология (неважно, в какой сфере она реализуется) жестко навязывает последовательность мероприятий и событий проекта, что и обуславливает соответствующий тип связи.
Ресурсные связи. В условиях назначения на один ответственный ресурс нескольких задач возникает его перегруженность, что может привести к удорожанию проекта

За счет подведения под менее критичную задачу дополнительного ресурса этого можно избежать, и такие связи называются ресурсными.

В момент формирования расписания проекта сначала применяются жесткие, а затем – мягкие связи. Далее, по необходимости, некоторые мягкие связи подлежат сокращению. Благодаря этому может быть достигнуто некоторое сокращение общей длительности проекта. В условиях перегруженности некоторых ответственных ресурсов из-за параллельных работ допустимо разрешение возникших конфликтов введением ресурсных связей. Однако следует контролировать, чтобы новые связи не привели к значительным изменениям общего плана.

Сопряженные работы как некая последовательность проектной задачи связаны друг с другом. Назовем их операциями А и В. Введем понятие отношения предшествования, которое рассматривается как некое ограничение на сроки и общую продолжительность, так как операция В не может начаться до момента окончания операции А. Это означает, что В и А связаны отношением простого предшествования, при этом вовсе не обязательно, чтобы В начиналось одномоментно с окончанием А. Например, отделочные работы начинаются после возведения крыши дома, но это не означает, что выполняться они должны в тот же момент, когда наступит указанное событие.