Построение модели множественной регрессии в ms excel

Как рассчитать коэффициент корреляции

Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.

Способ 1. Определение корреляции с помощью Мастера Функций

Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:

1. С помощью левой кнопки мыши выделяем ту ячейку, в которой будет находиться получившийся коэффициент корреляции. После этого находим слева от строки формул кнопку fx, которая откроет инструмент ввода функций. 
2. Далее выбираем категорию «Полный алфавитный перечень», в котором ищем функцию КОРРЕЛ. Как видно из названия категории, все названия функций располагаются в алфавитном порядке. 
3. Далее открывается окно ввода параметров функции. У нас два основных аргумента, каждый из которых являет собой массив данных, которые сравниваются между собой. В поле «Массив 1» указываем координаты первого диапазона, а в поле «Массив 2» – адрес второго диапазона. Для ввода данных массива, используемого для расчета, достаточно выделить нажать левой кнопкой мыши по соответствующему полю и выделить правильный диапазон. 
4. После того, как мы введем данные в аргументы, нажимаем кнопку «ОК», чем подтверждаем совершенные действия.

После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов. 

Способ 2. Вычисление корреляции с помощью пакета анализа

Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:

1. Нажимаем на кнопку «Файл», которая находится в левом верхнем углу сразу возле вкладки «Главная». 
2. После этого открываем раздел с настройками. 
3. В меню слева переходим в предпоследний пункт, озаглавленный, как «Надстройки». Делаем левый клик по соответствующей надписи. 
4. Открывается окно управления надстройками. Нам нужно переключить поле ввода, находящееся внизу, на пункт «Надстройки Excel» и нажать на «Перейти». Если это поле уже находится в таком положении, то не выполняем никаких изменений. 
5. Затем включаем пакет анализа в настройках. Для этого ставим соответствующую галочку и нажимаем на кнопку «ОК». 

Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее. 

Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК». 

Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».

Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».

В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».

Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более. 

Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.

Линейная регрессия в программе Excel

Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.

Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.

Линейная регрессия в программе Excel

Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.

Общее уравнение регрессии линейного вида выглядит следующим образом: . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.

1. Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».

Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».

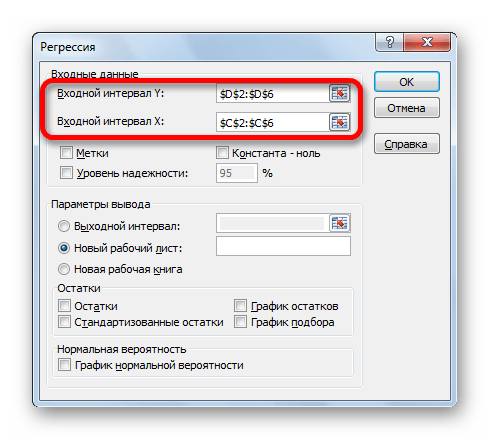
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.

В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.

В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».

С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно

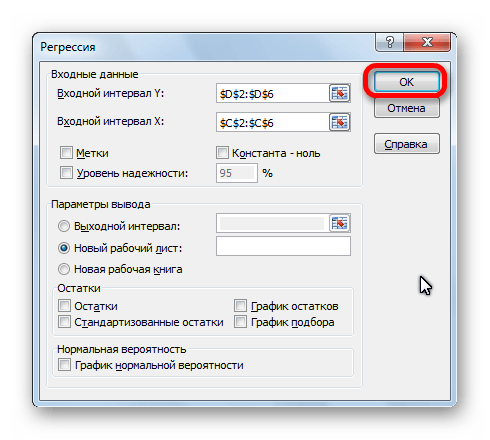
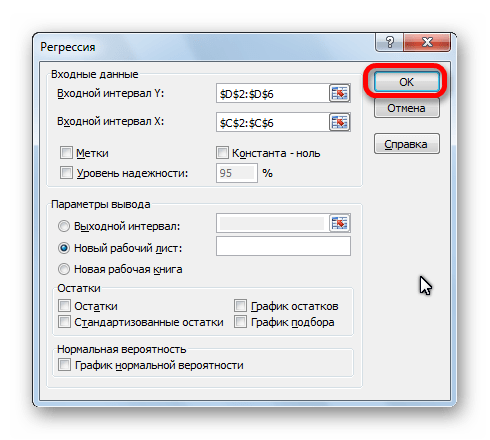
Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле

После того, как все настройки установлены, жмем на кнопку «OK».

Корреляционно-регрессионный анализ

На практике эти две методики часто применяются вместе.

Пример:

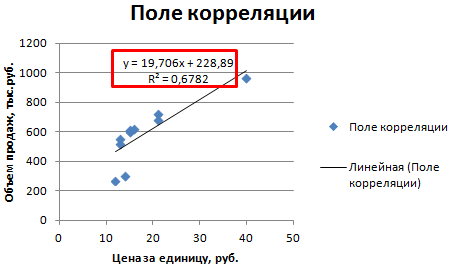
Теперь стали видны и данные регрессионного анализа.

Пакет MS Excel позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро

Важно понять, как интерпретировать полученные результаты

Для работы необходима надстройка Пакет анализа , которую необходимо включить в пункте меню Сервис\Надстройки

В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel , нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel » внизу окна:

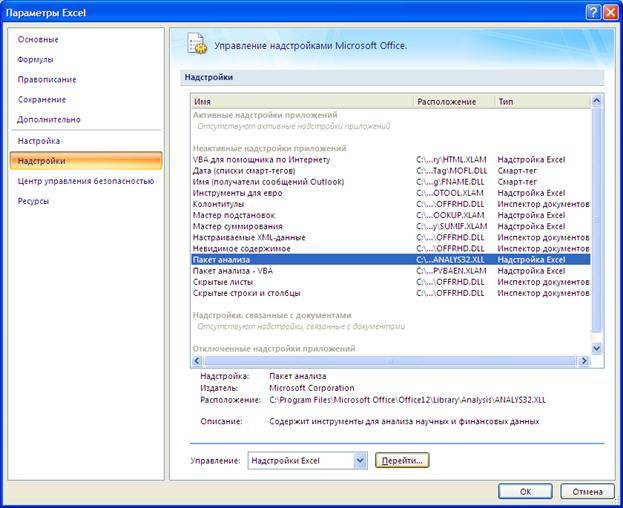
Для построения модели регрессии необходимо выбрать пункт Сервис\Анализ данных\Регрессия . (В Excel 2007 этот режим находится в блоке Данные/Анализ данных/ Регрессия ). Появится диалоговое окно, которое нужно заполнить:

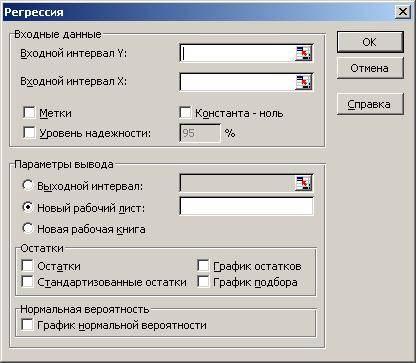
1) Входной интервал Y ¾ содержит ссылку на ячейки, которые содержат значения результативного признака y . Значения должны быть расположены в столбце;

2) Входной интервал X ¾ содержит ссылку на ячейки, которые содержат значения факторов . Значения должны быть расположены в столбцах;

3) Признак Метки ставится, если первые ячейки содержат пояснительный текст (подписи данных);

4) Уровень надежности ¾ это доверительная вероятность, которая по умолчанию считается равной 95%. Если это значение не устраивает, то нужно включить этот признак и ввести требуемое значение;

5) Признак Константа-ноль включается, если необходимо построить уравнение, в котором свободная переменная ;

6) Параметры вывода определяют, куда должны быть помещены результаты. По умолчанию строит режим Новый рабочий лист ;

7) Блок Остатки позволяет включать вывод остатков и построение их графиков.

В результате выводится информация, содержащая все необходимые сведения и сгруппированная в три блока: Регрессионная статистика , Дисперсионный анализ , Вывод остатка . Рассмотрим их подробнее.

1. Регрессионная статистика :

множественный R определяется формулой (коэффициент корреляции Пирсона );

R (коэффициент детерминации );

Нормированный R -квадрат вычисляется по формуле (используется для множественной регрессии);

Стандартная ошибка S вычисляется по формуле ;

Наблюдения ¾ это количество данных n .

2. Дисперсионный анализ , строка Регрессия :

Параметр df равен m (количество наборов факторов x );

Параметр SS определяется формулой ;

Параметр MS определяется формулой ;

Статистика F определяется формулой ;

Значимость F . Если полученное число превышает , то принимается гипотеза (нет линейной взаимосвязи), иначе принимается гипотеза (есть линейная взаимосвязь).

3. Дисперсионный анализ , строка Остаток :

Параметр df равен ;

Параметр SS определяется формулой ;

Параметр MS определяется формулой .

4. Дисперсионный анализ , строка Итого содержит сумму первых двух столбцов.

5. Дисперсионный анализ , строка Y-пересечение содержит значение коэффициента , стандартной ошибки и t -статистики .

P -значение ¾ это значение уровней значимости, соответствующее вычисленным t -статистикам. Определяется функцией СТЬЮДРАСП(t -статистика; ). Если P -значение превышает , то соответствующая переменная статистически незначима и ее можно исключить из модели.

Нижние 95% и Верхние 95% ¾ это нижние и верхние границы 95-процентных доверительных интервалов для коэффициентов теоретического уравнения линейной регрессии. Если в блоке ввода данных значение доверительной вероятности было оставлено по умолчанию, то последние два столбца будут дублировать предыдущие. Если пользователь ввел свое значение доверительной вероятности, то последние два столбца содержат значения нижней и верхней границы для указанной доверительной вероятности.

6. Дисперсионный анализ , строки содержат значения коэффициентов, стандартных ошибок, t -статистик, P -значений и доверительных интервалов для соответствующих .

7. Блок Вывод остатка содержит значения предсказанного y (в наших обозначениях это ) и остатки .

Суть корреляционного анализа

Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.

Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.

Основные задачи и виды регрессии

Регрессия представляет собой зависимость между заданными переменными, за счет чего можно определить прогноз будущего поведения данных переменных. Переменные — это различные периодические явления, включая и поведение человека. Такой анализ программы Excel применяется для того, чтобы проанализировать воздействие на конкретную зависимую переменную значений одной или некоторым количеством переменных. К примеру, на продажи в магазине влияет несколько факторов, включая ассортимент, цены и место локализации магазина. Благодаря регрессии в Excel можно определять степень влияния каждого из указанных факторов по результатам имеющихся продаж, а после применить полученные данные для прогнозирования продаж на другой месяц или для другого магазина, расположенного рядом.

Обычно регрессия представлена в виде простого уравнения, раскрывающего зависимости и силу связи между двумя группами переменных, где одна группа является зависимой или эндогенной, а другая — независимой или экзогенной. При наличии группы взаимосвязанных показателей зависимая переменная Y определяется исходя из логики рассуждений, а остальные выступают в роли независимых Х-переменных.

Основные задачи построения регрессионной модели заключаются в следующем:

1. Отбор значимых независимых переменных (Х1, Х2, …, Xk).
2. Выбор вида функции.
3. Построение оценок для коэффициентов.
4. Построение доверительных интервалов и функции регрессии.
5. Проверка значимости вычисленных оценок и построенного уравнения регрессии.

Регрессионный анализ бывает нескольких видов:

• парный (1 зависимая и 1 независимая переменные);
• множественный (несколько независимых переменных).

Уравнения регрессии бывает двух видов:

1. Линейные, иллюстрирующие строгую линейную связь между переменными.
2. Нелинейные — уравнения, которые могут включать степени, дроби и тригонометрические функции.

Инструкция построения модели

Чтобы выполнить заданное построение в Excel, необходимо следовать указаниям:

Для дальнейшего вычисления следует использоваться функцию «Линейн ()», указывая Значения Y, Значения Х, Конст и статистику. После этого определите множество точек на линии регрессии с помощью функции «Тенденция» — Значения Y, Значения Х, Новые значения, Конст. При помощи заданных параметров вычислите неизвестное значение коэффициентов, опираясь на заданные условия поставленной задачи.

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ В MS EXCEL

1. Создайте файл исходных данных в MS Excel (например, таблица 2)

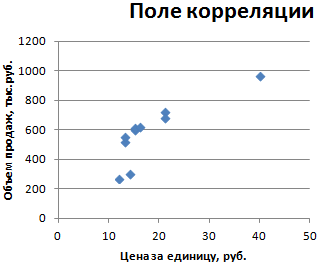
2. Построение корреляционного поля

Для построения корреляционного поля в командной строке выбираем меню Вставка/ Диаграмма . В появившемся диалоговом окне выберите тип диаграммы: Точечная ; вид: Точечная диаграмма , позволяющая сравнить пары значений (Рис. 22).

Рисунок 22 – Выбор типа диаграммы

Рисунок 23– Вид окна при выборе диапазона и рядов Рисунок 25 – Вид окна, шаг 4

2. В контекстном меню выбираем команду Добавить линию тренда.

3. В появившемся диалоговом окне выбираем тип графика (в нашем примере линейная) и параметры уравнения, как показано на рисунке 26.

Нажимаем ОК. Результат представлен на рисунке 27.

Рисунок 27 – Корреляционное поле зависимости производительности труда от фондовооруженности

Аналогично строим корреляционное поле зависимости производительности труда от коэффициента сменности оборудования. (рисунок 28).

от коэффициента сменности оборудования

3. Построение корреляционной матрицы.

Для построения корреляционной матрицы в меню Сервис выбираем Анализ данных.

С помощью инструмента анализа данных Регрессия , помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Для этого необходимо проверить доступ к пакету анализа. В главном меню последовательно выберите Сервис/ Надстройки . Установите флажок Пакет анализа (Рисунок 29)

Рисунок 30 – Диалоговое окно Анализ данных

После нажатия ОК в появившемся диалоговом окне указываем входной интервал (в нашем примере А2:D26), группирование (в нашем случае по столбцам) и параметры вывода, как показано на рисунке 31.

Результат расчетов представлен в таблице 4.

Использование Пакета анализа EXCEL для построения множественной линейной регрессионной модели

Проведем множественный регрессионный анализ с помощью надстройки MS EXCEL Пакет анализа .

Эффективно использовать надстройку Пакет анализа могут только пользователи знакомые с теорией множественного регрессионного анализа .

В данной статье решены следующие задачи:

• Показано как в MS EXCEL выполнить регрессионный анализ с помощью надстройки Пакет анализа (инструмент Регрессия), т.е. как вызвать надстройку и правильно заполнить входные данные;
• Даны пояснения по разделам отчета, формированного надстройкой;
• Даны комментарии обо всех показателях, рассчитанных надстройкой, и приведены ссылки на соответствующие разделы статей, посвященные простой линейной регрессии .

В надстройке Пакет анализа для построения линейной регрессионной модели (как простой , так и множественной ) имеется специальный инструмент Регрессия .

После выбора этого инструмента откроется окно, в котором требуется заполнить следующие поля (см. файл примера лист Надстройка ):

• Входной интервалY : ссылка на массив значений переменной Y. Ссылку можно указать с заголовком. В этом случае, при выводе результатов надстройка использует Ваш заголовок (для этого в окне требуется установить галочку Метки );
• Входной интервал Х : ссылка на значения переменных Х (нужно указать все столбцы со значениями Х). Ссылку рекомендуется делать на диапазон с заголовками (в окне не забудьте установить галочку Метки );
• Константа-ноль : если галочка установлена, то надстройка подбирает плоскость регрессии с b =0;
• Уровень надежности : Это значение используется для построения доверительных интервалов для наклона и сдвига . Уровень надежности = 1- альфа . Если галочка не установлена или установлена, но уровень значимости = 95%, то надстройка все равно рассчитывает границы доверительных интервалов, причем дублирует их. Если галочка установлена, а уровень надежности отличен от 95%, то рассчитываются 2 доверительных интервала : один для 95%, другой для введенного значения. Для демонстрации вышесказанного введем 90%;
• Выходной интервал: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона;
• Остатки : будут вычислены остатки модели , т.е. разница между наблюденными и предсказанными значениями Yi для всех наблюдений n;
• Стандартизированные остатки : Вышеуказанные значения остатков будут поделены на значение их стандартного отклонения ;
• График остатков : Для каждой переменной X _j будет построена точечная диаграмма : значения остатков и соответствующее значение Х _ji (при прогнозировании на основании значений 2-х переменных Х будет построено 2 диаграммы (j=1 и 2));
• График подбора: Для каждой переменной X _j будут построены точечные диаграммы с двумя рядами данных : точки данных (X _ji ;Y _i ) и (X _ji ;Y _{iпредсказанное} );
• График нормальной вероятности: Будет построена точечная диаграмма с названием График нормального распределения . По сути — это график значений переменной Y, отсортированных по возрастанию .

В результате вычислений будет заполнен указанный Выходной интервал.

Тот же результат можно получить с помощью формул (см. файл примера лист Надстройка , столбцы I:T).

Результаты вычислений, выполненных надстройкой, полностью совпадают с вычислениями сделанными нами в статье про множественную линейную регрессию с помощью функций ЛИНЕЙН() , ТЕНДЕНЦИЯ() и др. Использование альтернативных формул помогает разобраться с алгоритмом расчета показателей регрессии.

Отчет, сформированный надстройкой, состоит из следующих разделов:

Задача о целесообразности покупки пакета акций

Множественная регрессия в Excel выполняется с использованием все того же инструмента «Анализ данных». Рассмотрим конкретную прикладную задачу.

Руководство компания «NNN» должно принять решение о целесообразности покупки 20 % пакета акций АО «MMM». Стоимость пакета (СП) составляет 70 млн американских долларов. Специалистами «NNN» собраны данные об аналогичных сделках. Было принято решение оценивать стоимость пакета акций по таким параметрам, выраженным в миллионах американских долларов, как:

• кредиторская задолженность (VK);
• объем годового оборота (VO);
• дебиторская задолженность (VD);
• стоимость основных фондов (СОФ).

Кроме того, используется параметр задолженность предприятия по зарплате (V3 П) в тысячах американских долларов.

Изучение результатов и выводы

«Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:

СП = 0,103*СОФ + 0,541*VO – 0,031*VK +0,405*VD +0,691*VZP – 265,844.

В более привычном математическом виде его можно записать, как:

y = 0,103*x1 + 0,541*x2 – 0,031*x3 +0,405*x4 +0,691*x5 – 265,844

Данные для АО «MMM» представлены в таблице:

Подставив их в уравнение регрессии, получают цифру в 64,72 млн американских долларов. Это значит, что акции АО «MMM» не стоит приобретать, так как их стоимость в 70 млн американских долларов достаточно завышена.

Как видим, использование табличного процессора «Эксель» и уравнения регрессии позволило принять обоснованное решение относительно целесообразности вполне конкретной сделки.

Теперь вы знаете, что такое регрессия. Примеры в Excel, рассмотренные выше, помогут вам в решение практических задач из области эконометрики.

Известна тем, что она полезна в разных областях деятельности, включая и такую дисциплину, как эконометрика, где в работе используется данная программная утилита. В основном все действия практических и лабораторных занятий выполняют в Excel, которая существенно облегчает работу, давая подробные объяснения тех или иных действий. Так, один из инструментов анализа «Регрессия» применяется с целью подбора графика для набора наблюдений за счет метода наименьших квадратов. Рассмотрим, что представляет собой данный инструмент программы и в чем заключается его польза для пользователей. Ниже также предоставлена краткая, но понятная инструкция построения регрессионной модели.

Вывод регрессии в Excel

Первым шагом в запуске регрессионного анализа в Excel является повторная проверка того, что установлен бесплатный плагин Excel для анализа данных. Этот плагин позволяет легко вычислять статистику. это нетребуется для построения графика линейной регрессии, но это упрощает создание таблиц статистики. Чтобы проверить, установлен ли он, выберите «Данные» на панели инструментов. Если опция «Анализ данных» является опцией, эта функция установлена ​​и готова к использованию. Если он не установлен, вы можете запросить эту опцию, нажав кнопку Office и выбрав «Параметры Excel».

Используя Data Analysis ToolPak, для создания регрессионного вывода достаточно нескольких щелчков мышью.

Независимая переменная входит в диапазон X.

С учетом доходности S & P 500, скажем, мы хотим знать, можем ли мы оценить силу и соотношение доходности акций Visa (V). Запас Visa (V) возвращает данные, заполняет столбец 1 как зависимую переменную. S & P 500 возвращает данные, заполняющие столбец 2 как независимую переменную.

1. Выберите «Данные» на панели инструментов. Появится меню «Данные».
2. Выберите «Анализ данных». Откроется диалоговое окно «Анализ данных — Инструменты анализа».
3. В меню выберите «Регрессия» и нажмите «ОК».
4. В диалоговом окне «Регрессия» щелкните поле «Диапазон ввода Y» и выберите данные зависимой переменной (доходность Visa (V)).
5. Щелкните поле «Input X Range» и выберите данные независимых переменных (S & P 500 возвращает).
6. Нажмите «ОК» для запуска результатов.