Значение синуса, косинуса, тангенса и котангенса: их графики, описание

Растяжение (сжатие) графика ВДОЛЬ оси ординат.Симметричное отображение графика относительно оси абсцисс

Структура второй части статьи будет очень похожа.

1) Если ФУНКЦИЯ  умножается на число , то происходит растяжение её графика вдоль оси ординат.

Правило: чтобы построить график функции , где , нужно график функции  растянуть вдоль оси  в  раз.

2) Если ФУНКЦИЯ умножается на число , то происходит сжатие её графика вдоль оси ординат.

Правило: чтобы построить график функции , где , нужно график функции  сжать вдоль оси  в   раз.

Догадайтесь, какую функцию я буду снова пытать =)

Пример 11

Построить графики функций .

Берём синусоиду за макушку/пятки:
И вытягиваем её вдоль оси   в 2 раза:
Период функции  не изменился и составляет , а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается: .

Теперь сожмём синусоиду вдоль оси   в 2 раза:
Аналогично, период  не изменился, но область значений функции «сплющилась» в два раза: .

Нет, у меня нет какого-то пристрастного отношения к синусоиде, просто я хотел продемонстрировать, чем отличаются графики функций  (Примеры №№1,3) от только что построенных собратьев . Постарайтесь ещё раз проанализировать и качественнее понять эти элементарные случаи.  Даже минимальные знания о преобразованиях графиков окажут вам неоценимую помощь в ходе решения других задач высшей математики!

И, конечно же, классический пример растяжения/сжатия параболы:

Пример 12

Построить графики функций .

Возьмём рога молодого оленя  и вытянем их вверх вдоль оси  в два раза: . Затем сожмём  вдоль оси ординат в 2 раза:
И снова заметьте, что значения функции  увеличиваются в 2 раза, а значения  уменьшаются во столько же раз (исключение составляет точка ).

Отпустим в тундру удивлённое животное и продолжим изучать умножение функции на число: . Случаи  не представляют интереса, поэтому рассмотрим отрицательные коэффициенты. Сначала распространённый частный случай :

Если ФУНКЦИЯ меняет знак на противоположный, то её график отображается симметрично относительно оси абсцисс.

Правило: чтобы построить график функции , нужно график  отобразить симметрично относительно оси .

Пример 13

Построить график функции

Отобразим синусоиду симметрично относительно оси :

Ещё более наглядно симметрия просматривается у следующей типовой функции:

Пример 14

Построить график функции

График функции  получается путём симметричного отображения графика  относительно оси абсцисс:
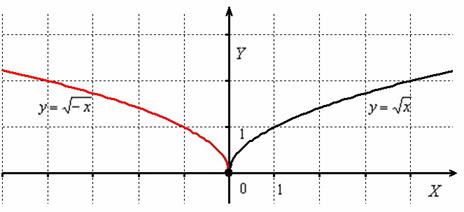
Функции  задают две ветви параболы, которая «лежит на боку». Обратная функция  задаёт параболу целиком. С подобными графиками часто приходится иметь дело при нахождении площадей фигур, построении областей интегрирования двойных интегралов и в некоторых других задачах.

При умножении функции на отрицательное число , , построение графика следует выполнить в два этапа: сжатие (или растяжение) вдоль оси ординат, а потом – симметричное отображение относительно оси абсцисс. Конкретные примеры увидим в следующем топике.

Построение графиков тригонометрических функций с использованием MS Excel

Тип урока: урок обобщения и систематизации знаний

Если вычислений много, а времени мало, то доверьтесь электронным таблицам

1. Сообщение целей и задач урока

– Ребята, сегодня мы продолжим знакомиться с возможностями электронных таблиц Excel. Давайте вспомним, для чего предназначены электронные таблицы? (Автоматизация расчетов). – Что вы уже умеете делать в электронных таблицах? (Создавать и форматировать таблицу, работать с типами данных, решать задачи используя относительную и абсолютную ссылки, строить диаграммы). – На уроках математики вы изучили тригонометрические функции и их графики. При построении графиков тригонометрических функций необходимо учесть множество нюансов. Начертить синусоиду или косинусоиду красиво – это уже искусство, а если необходимо график растянуть, сжать или симметрично отобразить относительно какой-либо оси – это может вызвать затруднения. И здесь нам на помощь нам придут электронные таблицы MS Excel. Вы узнаете как с их помощью быстро и красиво построить график. Сегодня на уроке мы познакомимся с алгоритмом построения графика тригонометрической функции. Эпиграфом к уроку я взяла слова «Если вычислений много, а времени мало, то доверьтесь электронным таблицам»

2. Актуализация знаний

На прошлом уроке вы строили графики элементарных функций. Давайте повторим алгоритм построения графика (Учащиеся называют шаги построения графика функции, а учитель показывает соответствующий пункт алгоритма на доске (используется проектор) и если необходимо дополняет ответ учеников) (см. Приложение 1).

3. Изучение нового

С использованием презентации (см. Приложение 2) учитель рассказывает, как строится график тригонометрической функций, а затем выполняет его построение в электронных таблицах.

4. Закрепление полученных знаний

Каждому ученику даётся карточка с заданием и оценочный лист, который после выполнения задания отдается учителю (Каждый пункт в оценочном листе является шагом построения графика тригонометрической функции с использованием MSExcel). Презентация находится в сетевой папке, и любой ученик может ею воспользоваться при выполнении своего задания.

5. Проверка построенных графиков и разбор нюансов

С помощью этого примера обращается внимание учащихся, что существуют функции, графики которых в электронных таблицах строятся неточно. Учащихся можно попросить найти неточности в графике, построенном с помощью MS Excel и попросить объяснить их

График, построенный традиционным алгебраическим

График, построенный с использованием МS Exel

6. Подведение итогов

Вывод. MS Excel облегчает построение графиков функций, но без глубоких математических знаний построить точные графики сложных функций (тригонометрических функций, функций с модулем, функций имеющих точки разрыва) невозможно.

Математика – это царица всех наук!

7. Постановка Д/З.

Свойство периодичности

Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.

Свойство периодичности

При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.

Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса. 

Математически данное свойство записывается так: 

sinα+2π·z=sin αcosα+2π·z=cos αtgα+2π·z=tg αctgα+2π·z=ctg α

Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов. 

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем примеры.

sin13π5=sin3π5+2π=sin3π5

tg(-689°)=tg(31°+360°·(-2))=tg31°tg(-689°)=tg(-329°+360°·(-1))=tg(-329°)

Таблица синусов и косинусов в Excel

Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

Заполним столбцы значениями углов в градусах:

Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

=COS(РАДИАНЫ(A2:A16))

Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

Аналогичным способом создадим таблицу синусов в Excel:

Список формул

Запишем формулы суммы и разности синусов и косинусов. Как Вы понимаете, их четыре штуки: две для синусов и две для косинусов.

Теперь дадим их формулировки. При формулировании формул суммы и разности синусов и косинусов угол называют полусуммой углов и , а угол – полуразностью. Итак,

• Формула суммы синусов : сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.
• Формула разности синусов : разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.
• Сумма косинусов : сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы на косинус полуразности этих углов.
• Формула разности косинусов : разность косинусов двух углов равна удвоенному произведению синуса полусуммы на синус полуразности этих углов, взятому со знаком минус.

Стоит отметить, что формулы суммы и разности синусов и косинусов справедливы для любых углов и .

Сжатие (растяжение) графика к (от) оси ординат.Симметричное отображение графика относительно оси

Первая группа действий связана с умножением АРГУМЕНТА функции на число. Для удобства я разобью правило на несколько пунктов:

Сжатие графика функции к оси ординат

Это случай когда АРГУМЕНТ функции умножен на число, бОльшее единицы.

Правило: чтобы построить график функции , где , нужно график функции  сжать к оси  в  раз.

И первой на эшафот взойдёт функция, которой я недавно грозился:

Пример 1

Построить график функции .

Сначала изобразим график синуса, его период равен :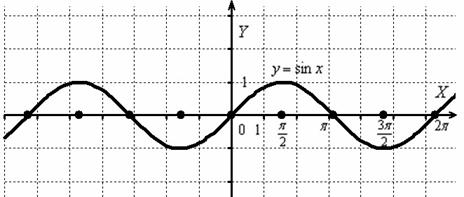
К слову, чертить графики тригонометрических функций вручную – занятие кропотливое, поскольку  и т.д., то есть на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра, даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.

Теперь поиграем на бесконечно длинном баяне. Мысленно возьмём синусоиду в руки и сожмём её к оси  в 2 раза:
То есть, график функции  получается путём сжатия графика  к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился:

В целях самоконтроля можно взять 2-3 значения «икс» и устно либо на черновике выполнить подстановку:
Смотрим на чертёж, и видим, что это действительно так.

Аналогичную блиц-проверку полезно осуществлять в любом другом примере! Более того, она лучше поможет усвоить суть того или иного преобразования.

Пример 2

Построить график функции

«Чёрная гармошка»  сжимается к оси  в 3 раза: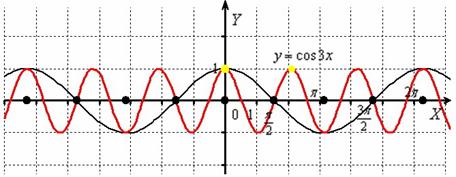
Итоговый график  проведён красным цветом.
Исходный период  косинуса закономерно уменьшается в три раза:  (отграничен жёлтыми точками).

Растяжение графика функции от оси ординат

Это противоположное действие, теперь баян не сжимается, а растягивается.
Случай имеет место, когда АРГУМЕНТ функции умножается на число .

Правило: чтобы построить график функции , где , нужно график функции  растянуть от оси  в  раз.

Продолжим мучить синус:

Пример 3

Построить график функции

Берём в руки нашу «бесконечную гармошку»:

И растягиваем её от оси  в 2 раза: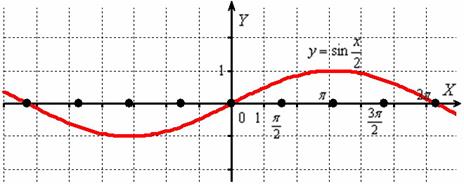

То есть, график функции  получается путём растяжения графика  от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза: , он толком даже не вместился на данный чертёж.

Операции сжатия/растяжения графиков, разумеется, выполнимы не только для тригонометрических функций:

Пример 4

Построить графики функций

График функции  получается путём сжатия графика экспоненты  к оси  в два раза. А график  – путём растяжения графика экспоненты  от оси  в два раза:

В качестве ассоциации можете опять поиграть на «баяне» .

Продолжаем систематизировать  умножение аргумента функции на число:
Мы рассмотрели два случая – сжатие () и растяжение ().

Очевидно, что нет практического смысла рассматривать значения . Есть более интересный вопрос: что происходит, когда аргумент умножается на отрицательное число? Ответ будет получен чуть позже, а пока рассмотрим распространённый частный случай, когда :

Симметричное отображение графика функции относительно оси ординат

АРГУМЕНТ функции меняет знак.

Правило: чтобы построить график функции , нужно график  отобразить симметрично относительно оси .

Наглядный пример уже встречался на уроке Графики и свойства элементарных функций (вспоминаем ). Распечатаем ещё один комплект:

Пример 5

Построить график функции

График функции  получается путём симметричного отображения графика  относительно оси ординат:

Как видите, всё просто.

Если при умножении аргумента на число  значение параметра  отрицательно и не равно минус единице, то построение выполняется в два шага. Например: . На первом шаге выполняем сжатие графика  к оси ординат в 2 раза: . На втором шаге график  отображаем симметрично относительно оси ординат: . Конкретный пример обязательно рассмотрим ниже.

А следующий параграф посвящается одному интересному человеку из дворовой компании моего далёкого детства. Он вытягивал руки в стороны, открывал рот и прыгал влево/вправо по проезжей части. Водители крутили виском у пальца, сигналили, но догнать его так никто и не смог.

π без картинок

Представьте себе слепого пришельца, который может различать только тени света и темноты. Можете ли вы объяснить ему, что такое π? Довольно сложно пояснить в такой ситуации понятие длины окружности, верно?

Давайте вернемся немного назад. Синус — это циклическая функция. Это означает, что значит ее значения должны…повторяться! Синус начинается с 0, идет к 1, к 0, к -1, к 0 и так далее.

Давайте определим π как время, за которое синус поднимается с 0 до 1, и обратно возвращается к 0. Вау! Теперь и мы используем π без всяких окружностей!

• Синус — это плавное передвижение вперёд-назад
• π — это время движения синуса с 0 до 1 и обратно до 0
• n * π (0 * π, 1 * π, 2 * π и т.д.) — это момент времени, в котором синус равен 0
• 2 * π, 4 * π, 6 * π и т.д. — полные периоды синуса.

Ага! Вот почему π встречается в таком количестве формул! π не «принадлежит» окружностям больше, чем 0 или 1 — π касается возвращения синуса в центр! Окружность — это пример фигуры, которая повторяется и возвращается в центр каждые 2*π единиц. Но вибрации, скачки и т.д. возвращаются к центру каждый π!

Вопрос: если π — это половина естественного периода, почему оно длится вечно (является иррациональным числом)?

Можно я отвечу вопросом на вопрос, А почему длина диагонали «единичной окружности» равна квадратному корню из 2, который также уходит в бесконечность?

Но да, я понимаю, что это философски не удобно, когда природа ведет себя произвольно. Но что поделаешь…

Использование формул

Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.

Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.

Пример 8

Найдите значение tgπ8 . 

Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22 

Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1

tgπ8=2-1.

Знаки тригонометрических функций по четвертям

Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?

Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A(1, ) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y). В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно. 

Для наглядности приведем иллюстрацию.

Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° — угол третьей четверти. Угол -45° —  это угол четвертой четверти.

При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.

Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.

Косинус — это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.

Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям. 

Важно помнить!

1. Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
2. Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
3. Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
4. Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.

7 Графики синуса и косинуса

Построим график функции . При этом нам опять пригодятся
часы из разд. 2.1.

Если , то, очевидно, . Когда возрастает от 0 до
, число возрастает от 0 до 1 (представьте себе,
как меняется ордината конца стрелки на наших фирменных часах).
Участок графика для от 0 до изображен на
рис. .
При

Чем ближе к , тем более полого идет наша кривая. Это
происходит потому, что проекция конца стрелки на ось
ординат, колеблясь по отрезку , быстрее всего
движется в середине отрезка и замедляется у его краев: мы
это уже обсуждали в разд. 2.1.

симметричны относительно прямой

Задача 7.1  
Запишите уравнение прямой, касающейся графика функции
в точке с координатами .

Кривая на рис б
центрально симметрична относительно точки
с координатами ; это следует из другой формулы
приведения:
(рис. б).

После того, как у нас есть участок графика функции для

, весь график строится уже просто. В самом деле,
когда конец стрелки прошел путь , стрелка вернулась
в исходное положение; при дальнейшем движении все будет
повторяться. Значит, график будет состоять из таких же кусков,
как на рис б. Окончательно график функции
выглядит так, как на рис. .

Теперь построим график функции . Можно было бы строить его так же, как
мы строили график синуса. Мы, однако, изберем другой путь,
который позволит использовать уже имеющуюся у нас информацию.

Именно, воспользуемся формулой приведения
. Эту формулу можно понимать так: функция
принимает те же значения, что и функция , но на
раньше. Например, функция принимает значение 1 при
, а функция
принимает это же
значение уже при . На графике это означает следующее: для
каждой точки графика есть точка графика ,
у которой ордината та же, а абсцисса на меньше
(рис. ).

сдвинуть график

Итак, мы выяснили, что график косинуса получается преобразованием
(сдвигом) из графика синуса. Случаи, когда график одной функции
можно получить преобразованием из графика другой функции,
интересны и сами по себе, поэтому скажем о них несколько слов.

Как, например, будет выглядеть график функции ? Ясно,
что ординаты точек этого графика получаются из ординат
соответствующих точек графика умножением на 2, так что
наш график изобразится сплошной кривой на рис. . Можно
сказать, что график получается из графика растяжением в два раза вдоль оси
ординат.

сжатием в 2 раза к оси ординат.

Попробуем еще построить график функции 
.
Понятно, что он должен получаться каким-то преобразованием из
графика . На первый взгляд может показаться, что это
преобразование — сдвиг влево на вдоль оси абсцисс, по
аналогии с тем, что изображено на рис. . Однако, если
бы это было так, то вышло бы, например, что функция

принимает значение 1 при

, что не соответствует действительности
(проверьте!). Правильно рассуждать так:
, так что функция
принимает те
же значения, что и функция , но на раньше. Так
что сдвиг влево — не на
, а на (рис. ).

Кривые, являющиеся графиками функций
, где ,
, называются синусоидами. Заметим, что кривой
«косинусоида» вводить не надо: как мы видели, график косинуса
— это та же кривая, что и график
синуса, только иначе
расположенная относительно осей координат.

Задача 7.2  
Каковы координаты точек, помеченных на
рис.  вопросительными знаками?

Задача 7.3  
Возьмите свечу, тонкий лист бумаги и острый нож. Намотайте лист
бумаги на свечу в несколько слоев и аккуратно разрежьте эту свечу
вместе с бумагой наискосок ножом. Теперь разверните бумагу. Вы
увидите, что она оказалась разрезанной по волнистой линии.
Докажите, что эта волнистая линия является синусоидой.

Задача 7.4  
Постройте графики функций:

Замечание. Если вы строите графики
тригонометрических функций на клетчатой бумаге, удобно выбрать
немного разные масштабы по осям, с тем чтобы на оси абсцисс
числу  соответствовало целое число клеточек. Например, часто
выбирают такой масштаб: по оси ординат отрезок длины 1 занимает
две клеточки, по оси абсцисс отрезок длины занимает 6
клеточек.

Задача 7.5  
Постройте графики функций:
а)
;
б)
.

Посмотрим, как выглядят на графиках уже известные нам решения
уравнений и . Эти решения являются
абсциссами точек пересечения горизонтальной прямой
с графиком функций (соответственно ). На
рис. , хорошо видны две серии решений,
получающихся при .

По графикам синуса и косинуса видно, на каких промежутках эти
функции возрастают, а на каких убывают. Ясно, например, что
функция возрастает на отрезках
,

,
,…- одним словом, на
всех отрезках
, где
,
и убывает на всех отрезках
, где

.

Задача 7.6  
На каких отрезках возрастает и на каких убывает
функция ?

Задача 7.7  
Сравните числа:

Задача 7.8  
Расположите в порядке возрастания:
, , , , , .

        Написать комментарий

4. Монотонность функции на промежутке [-π/2; π/2]

Важ­ней­шая осо­бен­ность функ­ции  на от­рез­ке  мо­но­тон­ность функ­ции. По­это­му и пря­мая и об­рат­ная за­да­чи тут имеют одно ре­ше­ние.

1. Пря­мая за­да­ча – за­дан­но­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет един­ствен­ное зна­че­ние функ­ции.

На­при­мер: 

2. Об­рат­ная за­да­ча – за­дан­ное зна­че­ние мо­но­тон­ной функ­ции до­сти­га­ет­ся толь­ко при одном зна­че­нии ар­гу­мен­та.

На­при­мер: Если 

Если 

Если 

За­да­ча 4. По­стро­ить гра­фик функ­ции 

Ре­ше­ние:

По­стро­им гра­фик функ­ции  В силу пе­ри­о­дич­но­сти до­ста­точ­но будет рас­смот­реть гра­фик на участ­ке 

Для по­лу­че­ния ис­ко­мо­го гра­фи­ка кри­вую  необ­хо­ди­мо сдви­нуть на  впра­во по оси x (рис. 6).

Вспом­ним общее пра­ви­ло: Кри­вая  по­лу­ча­ет­ся сдви­гом кри­вой  на  впра­во по оси x.

За­да­ча 5. Найти наи­боль­шее и наи­мень­шее зна­че­ния функ­ции  на от­рез­ке 

Ре­ше­ние (рис. 7).

Ответ: 

3. Решение типовых задач

Рас­смот­рим несколь­ко задач, при ре­ше­нии ко­то­рых очень важ­ное зна­че­ние имеет мо­но­тон­ность функ­ции.

За­да­ча 1.

a) Найти наи­боль­шее зна­че­ние функ­ции на от­рез­ке 

Ре­ше­ние:

Функ­ция мо­но­тон­но воз­рас­та­ет на ука­зан­ном про­ме­жут­ке, зна­чит, наи­боль­шее зна­че­ние при­ни­ма­ет на пра­вом конце от­рез­ка,   (рис. 3).

b) Найти наи­мень­шее зна­че­ние функ­ции  на от­рез­ке 

Ре­ше­ние:

Функ­ция мо­но­тон­но воз­рас­та­ет на ука­зан­ном от­рез­ке, зна­чит, наи­мень­шее зна­че­ние при­ни­ма­ет на его левом конце,   (рис. 3).

Ответ: a) 1;  b) 

За­да­ча 2. Если ар­гу­мент ме­ня­ет­ся в за­дан­ных пре­де­лах, то най­ди­те, в каких пре­де­лах ме­ня­ет­ся функ­ция . Найти наи­мень­шее и наи­боль­шее зна­че­ние функ­ции.

a) 

Ре­ше­ние:

Функ­ция  мо­но­тон­но воз­рас­та­ет на  от­рез­ке  зна­чит,

 (рис. 4).

Ответ: 

b) 

Ре­ше­ние:

На за­дан­ном про­ме­жут­ке функ­ция немо­но­тон­на (рис. 5).

На гра­фи­ке мы видим, что функ­ция ме­ня­ет­ся в пре­де­лах 

Ответ: 

За­да­ча 3. Найти ко­ли­че­ство ре­ше­ний урав­не­ния  на про­ме­жут­ке 

Ре­ше­ние:

На за­дан­ном про­ме­жут­ке функ­ция мо­но­тон­на, зна­чит, каж­дое свое зна­че­ние она при­ни­ма­ет при един­ствен­ном зна­че­нии ар­гу­мен­та (рис. 1). По­это­му урав­не­ние на дан­ном от­рез­ке имеет един­ствен­ное ре­ше­ние.

Тригонометрический круг

Графически соотношение упомянутых величин можно представить следующим образом:

Окружность, в данном случае, представляет собой все возможные значения угла α – от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.

Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.

Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.

Данные углы выбраны отнюдь не случайно. Обозначение π  в таблицах стоит для радиан. Рад  – это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.

Углы в таблицах для тригонометрических функций соответствуют значениям радиан:

Итак, не трудно догадаться, что 2π – это полная окружность или 360°.