Как считать проценты в excel

Критерии к оценке

Для того, чтобы выбрать выгодный и в то же время надежный банк для вкладов, необходимо оценить ряд важнейших показателей, а не одну лишь процентную ставку и прибыльность вклада. Именно поэтому имеет смысл разобраться с процессом сравнения прогнозированных значений, которые мы получаем в результате расчетов.

Для начала, давайте определимся с тем, что ставка по вкладу представляет собой тариф вознаграждения, выраженный в процентах, на которое вы вправе рассчитывать, размещая свои сбережения в выбранном банке в выбранном вкладе. Как правило, банки считают размер ставки в виде годовых процентов

На этом моменте я хочу акцентировать ваше внимание. Ведь далеко не всегда мы кладем деньги на депозитных счет на целый год

Вполне допустимо открыть вклад на 1, 3 или 6 месяцев, или на срок свыше одного года. В таком случае нас интересует размер ежемесячного вознаграждения за открытый вклад. Чтобы узнать доходность вклада, открытого на несколько месяцев, нам нужно привести заявленную в договоре ставку к реальному сроку нашего вклада.

Сделать это совсем не сложно, и вам вполне хватит вашего школьного курса алгебры, в рамках которого вы изучали проценты. Всем нам известно, что 1 копейка – это один процент от рубля. В свою очередь рубль – это один процент от ста рублей. Иными словами, за один процент принимается сотая часть любого числа.

К примеру: 1% от суммы в 10 000 рублей – это 100 рублей. Вроде бы ничего сложного, правда? Но как считать эти суммы для временных периодов, если процент указан за год?

Годовой процент

Сразу стоит ввести новый термин – годовой процент, которым мы будет называть размер вознаграждения, которое получит вкладчик от банка за то, что его деньги будут храниться в виде депозита один год. Если перевести эту фразу в числовое значение, то получается, что, открывая вклад на сумму в 10 000 рублей сроком на один год по 15% годовых, по прошествии расчетного периода мы получим уже не 10 000 рублей, а 11 500.

Но что делать, если у вас с банком нестандартное условие хранения средств, которое подразумевает открытие вклада не на полгода или год, а, к примеру, на 370 или 395 дней? Согласитесь, довольно необычное календарное исчисление? Скорее всего, такое предложение сопровождается еще и довольно высокими процентными ставками, которые при перерасчете практически не будут отличаться от всех остальных предложений на рыке.

Заказывайте карту Открытие с начислением % на остаток

Расчёт

Чтобы перепроверить правдивость моих слов, вам необходимо выяснить, какой доход вы получите за один день хранения денег на депозите. Предположим, что наш вклад открыт на 370 дней, а сумма вознаграждения из предыдущего примера равнялась 1500 рублям. Исходя из этих данных, получаем, что один день работы вашего вклада принесет вам

1500 : 365 = 4 рубля и 11 копеек

Теперь считаем, что мы получим, если пойдем на поводу у рекламы

1500 : 370 = 4 рубля и 5 копеек

Таким образом, получается, что 6 копеек – это всего-навсего маркетинговый фокус

Исходя из этого, мы можем сделать вполне закономерный вывод, — обращать внимание при открытии депозита нужно не только на обещанные дивиденды, а еще и на условия

Пример использования сложных процентов

Далее выведем прибыльность сберегательного вклада с тем же условием, как и в предыдущем примере. Исключение составляет применение метода капитализированного процента.

Задача № 2

Условия депозита:

• Вложение — от 30 000 рублей.
• Депозитный срок — 6 месяцев (декабрь-май).
• Периодичность начисления и выплаты процентов — ежемесячно с капитализацией.
• Ставка по вкладу — 8,7 % годовых.

Алгоритм расчета приведен в таблице ниже.

Месяц	Сумма, рублей	Количество дней	Проценты	Итог по месяцам, рублей
1-й месяц	30 000	31	8,7 : (100 х 365)	221,67
2-й месяц	30 000 + 221,67	31	8,7 : (100 х 365)	223,31
3-й месяц	30 221,67 + 223,31	28	8,7 : (100 х 365)	203,19
4-й месяц	30 444,98 + 203,19	31	8,7 : (100 х 365)	226,46
5-й месяц	30 648,17 + 226,46	30	8,7 : (100 х 365)	220,77
6-й месяц	30 874,63 + 220,77	31	8,7 : (100 х 365)	229,77

В итоге спустя полгода сумма сложных процентов стала равной 1325,17 руб., итоговая сумма вклада с процентами — 31 325,17 руб. Таким образом, вклад с капитализацией процентов за 6 месяцев принес дополнительный доход в размере 30,87 руб.

Расчет годового процента по займу производился бы тем же путем. В ситуации взятия кредита или обращения в мелкие финансовые организации, такие как МФО, процентные начисления производятся таким же способом. Отличие заключается в формулировке названия. В случае депозита – это доходность, в случае кредита – это комиссии клиента или доходность самого банка.

Простые и сложные %

Рассмотрим ещё тип задач, относящихся к финансовым и связанных с процентами. Это такие задачи, в которых нужно вычислять доход от вклада или инвестиций. Вот такой пример. Вы вложили деньги в банк под р % годовых некую сумму S0. Чему будет равен ваш капитал через n лет? И ответ на этот вопрос зависит от того, какой у вас вклад: с простым начислением процентов или с их капитализацией.

Простое начисление процентов — это ежегодное (ежеквартальное, ежемесячное) получение р % от суммы вашего вклада, когда начальная сумма вклада S0 фиксирована, а вы регулярно с этой суммы получаете фиксированный доход, то есть каждый год (квартал, месяц) вы получаете прибыль 0,01p•S0. Через n лет ваша прибыль станет равна 0,01nр•S0. Полученная прибыль суммируется с вашим начальным вкладом S0, в результате чего вся сумма прибыли вместе с процентами составит:

S=S0•(1+0,01np). (4).

Задача. Вы положили 100000 рублей в банк под 10% годовых на 5 лет. Чему станет равен ваш вклад?

Решение: S=100000•(1+0,01•5•10)=100000•1,5=150000 рублей.

Допустим теперь, что ваш вклад с капитализацией процентов. Это означает, что после каждого начисления проценты прибавляются к уже имеющейся сумме на вашем счету. Таким образом, после следующего начисления сумма процентов становится больше. Например, в первый год проценты по вкладу с капитализацией составят 0,01р•S0, а за второй год эта сумма будет уже больше и составит 0,01p•(S0+0,01p•S0)=0,01p•S0•(1+0,01р), а за третий год — 0,01p•(S0+0,01p•S0•(1+0,01р))=0,01р•S0•(1+0,01p+(0,01p)²).

Выражение в скобках представляет собой сумму геометрической прогрессии, которая равна (0,01р)². Поэтому за третий год сумма на вашем счету станет равной S0+S0•(0,01р)³. Продолжая так дальше, через n лет или периодов начисления, сумма на счету вместе с начисленными процентами составит:

S=S0•(1+0,01р)ⁿ. (5).

Мы получили так называемую формулу сложных процентов, которая позволяет высчитывать сумму на вашем счету по вкладу с капитализацией процентов.

Задача. Вы положили всё те же 100 000 рублей на 5 лет под 10 % годовых, но открыли вклад с капитализацией. Сколько к концу указанного срока будет на вашем счету?

Решение. Пользуясь формулой сложных процентов, получим: S=100000•(1+0,01•10)^5=100000•1,1^5=100000•1,61051=161051 рубль.

Сравнивая результаты, полученные по формулам (4) и (5), видим, что по вкладу с капитализацией сумма на счету стала больше на 11051 рубль по сравнению с обычным вкладом, где происходит простое начисление процентов. Таким образом, второй способ вложения денег выгоднее.

Использование процентов на практике

Как рассчитывать проценты, каждый из нас знает еще из школьного курса математики. В повседневной жизни мы сталкиваемся с процентными соотношениями чуть ли не каждую минуту. Любая хозяйка, готовя какое-то блюдо, использует рецептуру, в которой представлено именно процентное соотношение. Самый простой пример: берем полстакана молока… Это и есть математическая трактовка того, что представляет собой определенная часть по отношению к целой.

За основу абсолютно всех вычислений принято считать 100 процентов (100%) или единицу (1), если расчет будет производиться с использованием дробей. От этого и отталкиваются при вычислении какой-либо составляющей от начального показателя.

То же самое касается и вопроса о том, как посчитать процент от суммы, когда в качестве начального (100-процентного) показателя выступает не одно число, а несколько. Вариантов расчета здесь может быть достаточно много. Рассмотрим самые основные.

Вычисление процентов по пропорции

Сейчас мы не будем брать в расчет вычисление процентов с использованием тех же таблиц офисных программ типа Excel, которые делают это в автоматическом режиме при задании соответствующей формулы.

В некоторых случаях используется калькулятор, на котором можно задавать вычисление подобных действий. Но речь сейчас не об этом.

Рассмотрим наиболее распространенные способы вычислений, знакомые нам из школьного курса математики.

Простейшим и самым распространенным способом является решение пропорции.

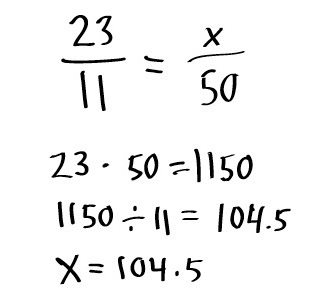
В данном случае исходное число задается в виде 100 процентов (скажем, некое произвольное число «a»), а его часть (допустим, «b») – в виде неизвестной «x». В математике это выглядит так:

Исходя из правил пропорции, можно вычислить неизвестное число x. Для этого используется так называемый перекрестный метод. Иными словами, нужно умножить b на 100 и разделить на a. Точно такое же правило действует, если в случае составления пропорции поменять b и x местами, когда процент известен, а нужно вычислить часть в числовом выражении.

Формула простых процентов.

Она используется тогда, когда начисляемый доход присоединяется к основному телу депозита в конце его срока или не присоединяется и выводится на текущий счет или пластиковую карточку. Этот порядок расчета стоит учесть, когда размещается солидная сумма на длительный срок. Обычно в данном случае банки применяют варианты размещения без капитализации, что понижает общую выгоду вкладчика.

Формула простого %:
Сумма % — это  доход, полученный через i-ый промежуток времени.

Р – изначальный объем вложений.

i – депозитная годовая ставка.

t – срок вложения.

T – число дней в году.

Рассмотрим пример: разместим 100 000 рублей на полгода под 12%. Рассчитаем полученный доход:

Таким образом, через полгода со счета можно будет снять 105 950,68 руб.

Расчет процентов на банковский депозит. Формула расчета простых процентов.

Если проценты на депозит начисляются один раз в конце срока депозита, то сумма процентов вычисляется по формуле простых процентов.

S = K + (K*P*d/D)/100 Sp = (K*P*d/D)/100

Где: S — сумма банковского депозита с процентами, Sp — сумма процентов (доход), K — первоначальная сумма (капитал), P — годовая процентная ставка, d — количество дней начисления процентов по привлеченному вкладу, D — количество дней в календарном году (365 или 366).

Пример 1. Банком принят депозит в сумме 100 тыс. рублей сроком на 1 год по ставке 20 процентов.

S = 100000 + 100000*20*365/365/100 = 120000 Sp = 100000 * 20*365/365/100 = 20000

Пример 2. Банком принят депозит в сумме 100 тыс. рублей сроком на 30 дней по ставке 20 процентов.

S = 100000 + 100000*20*30/365/100 = 101643.84 Sp = 100000 * 20*30/365/100 = 1643.84

Как рассчитать разные платежи по кредиту

Существует две схемы, по которым рассчитываются займы в банке — аннуитетная и дифференцированная. Первый вариант предусматривает более дорогие кредиты, поскольку процент начисляется на весь объем ссуды. Второй вариант подразумевает процентную ставку по кредиту с учетом предыдущих выплат, поэтому такой заем будет немного дешевле. Можно пересчитать ссуду по двум формулам — аннуитетной и дифференцированной и убедиться в этом лично.

Оформить дифференцированный заем намного сложнее, поскольку банки теряют на этом свой заработок. В том случае, когда это удается, нужно внимательно прочитать договор и убедиться, что отсутствуют дополнительные платежи, которыми кредитор захочет компенсировать потерянные деньги.

Изучая кредитную информацию, заемщикам необходимо внимательно ознакомиться с требованиями и условиями банков. Во время подписания бумаг стоит перечитать все пункты и задать интересующие вопросы по полученному договору. Также стоит перепроверить ежемесячные платежи, размер которых вычисляется по формулам, указанным выше.

Аннуитетные платежи

Аннуитетные платежи подразумевают наличие выплат равными частями на протяжении всего срока кредитования. Обязательный взнос, который необходимо перечислять на счет кредитора, состоит из двух частей — тела и процентов от суммы кредита. Такой способ расчета в интересах банка, поэтому аннуитетные займы предоставляются в большинстве кредитных организаций и имеют оптимальную годовую ставку.

Правильно рассчитать взнос по аннуитетной схеме легче, поскольку весь долг делится на равные части. Определить объемы выплат и сравнить результат с графиком, выданным банком, должен каждый заемщик. Это позволит избежать таких ситуаций, когда клиент погасил весь заем, а некоторая задолженность осталась

Важно мониторить свой счет, платеж сохранять в личном кабинете или распечатывать квитанцию

Дифференцированные платежи

Дифференцированная система кредитования подразумевает изменение ежемесячных выплат в зависимости от остатка долга. Тело займа разделяется на равные части исходя из количества платежей, а процент высчитывается от объема средств, которые остались для погашения. Таким образом, с каждым месяцем кредитные выплаты, которые необходимо осуществить заемщику, уменьшаются.

Кредиторы редко используют дифференцированную систему, поскольку она снижает стоимость займа. Кроме того, при дифференцированном расчете проще погасить долг досрочно, что значит — меньше будет заработок у банковских компаний. Финансовым структурам выгоднее получать стабильный доход в месяц, чем предоставлять недорогое кредитование.

Для подсчета выплат в рамках дифференцированного кредитования лучше использовать таблицу, в которую будет занесена определенная сумма долга каждый месяц на весь срок займа. Какой бы репутацией ни славился банк, необходимо самостоятельно перепроверить график платежей и удостовериться, что нет никаких ошибок.

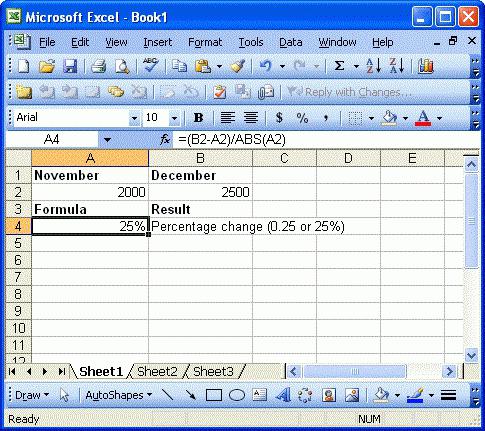
Расчет процентов в Excel.

Основная формула для расчета процента от числа в Excel такая же, как и во всех сферах жизни:

Часть / Целое = Процент

Если вы сравните ее с основной математической формулой для процента, которую мы указали чуть выше, то  заметите, что в формуле процента в Excel отсутствует часть * 100. При вычислении процента в Excel вам совершенно не обязательно умножать полученную дробь на 100, поскольку программа делает это автоматически, когда процентный формат применяется к ячейке.

И если в Экселе вы будете вводить формулу с процентами, то можно не переводить в уме проценты в десятичные дроби и не делить величину процента на 100. Просто укажите число со знаком %.

То есть, вместо =A1*0,25   или =A1*25/100 просто запишите формулу процентов  =A1*25%.

Хотя с точки зрения математики все 3 варианта возможны и все они дадут верный результат.

А теперь давайте посмотрим, как можно использовать формулу процента в Excel для реальных данных. Предположим, в вашей таблице Эксель записана сумма заказанных товаров в столбце F и оставленных товаров в столбце G. Чтобы высчитать процент доставленных товаров, выполните следующие действия:

• Введите формулу =G2/F2 в ячейку H2 и скопируйте ее на столько строк вниз, сколько вам нужно.
• Нажмите кнопку «Процентный стиль» ( меню «Главная» > группа «Число»), чтобы отобразить полученные десятичные дроби в виде процентов.
• Не забудьте при необходимости увеличить количество десятичных знаков в полученном результате.
• Готово! 🙂

Такая же последовательность шагов должна быть выполнена при использовании любой другой формулы процентов в Excel.

На скриншоте ниже вы видите округленный процент доставленных товаров без десятичных знаков.

Чтобы определить процент доставки, мы сумму доставленных товаров делим на сумму заказов. И используем в ячейке процентный формат, при необходимости показываем десятичные знаки.

Запишите формулу в самую верхнюю ячейку столбца с расчетами, а затем протащите маркер автозаполнения вниз по столбцу. Таким образом, мы посчитали процент во всём столбце.

Использование процентов на практике

Как рассчитывать проценты, каждый из нас знает еще из школьного курса математики. В повседневной жизни мы сталкиваемся с процентными соотношениями чуть ли не каждую минуту. Любая хозяйка, готовя какое-то блюдо, использует рецептуру, в которой представлено именно процентное соотношение. Самый простой пример: берем полстакана молока… Это и есть математическая трактовка того, что представляет собой определенная часть по отношению к целой.

За основу абсолютно всех вычислений принято считать 100 процентов (100%) или единицу (1), если расчет будет производиться с использованием дробей. От этого и отталкиваются при вычислении какой-либо составляющей от начального показателя.

То же самое касается и вопроса о том, как посчитать процент от суммы, когда в качестве начального (100-процентного) показателя выступает не одно число, а несколько. Вариантов расчета здесь может быть достаточно много. Рассмотрим самые основные.

Как правильно рассчитать проценты по кредиту – пример

10000 * 12% = 1200 рублей составит сумма, которую необходимо выплатить за пользование процентами банку.

То есть, если из наших 10000 выплачено 5000, то: 5000 * 12%/12 = 50 рублей ежемесячно придется отдавать банку за пользование кредитом. При этом, помножив это же число на 12, получим среднюю сумму для оплаты процентов за весь год.

При обращении в банк для получения кредита следует уточнить, какая система кредитования работает в данной организации. Если предлагается сделать выбор самостоятельно, то есть смысл остановиться на дифференцированном платеже. По такому платежу меньше переплата, да и само осознание того, что платить приходится за свои деньги, является немаловажным фактором при выборе способа кредитования.

Ипотечные кредиты также выгодно выплачивать дифференцированно, так как при растущей стоимости недвижимости невыгодно выплачивать кредит с переплатой значительной суммы средств.

Рассмотрим пример, который поможет правильно рассчитать кредит самому. Для простоты возьмём целые числа и округлим полученный результат до целого значения.

Кредит был оформлен на сумму 12000 рублей и выбрана была дифференцированная система погашения.

Товар был условно куплен в декабре, значит следующий срок платежа датирован январем будущего года.

Срок кредита – 1 год, ставка по проценту – 10%.

Месяц	Сумма основного долга	Расчет процентов	Итого к оплате
Январь	12000	12000*12*31/100*365=122	12122
Февраль	11000	11000*12*28/100*365=101	11101
Март	10000	10000*12*31/100*365=102	10102
Декабрь	1000	1000*12*31/100*365=10	1010

Период с апреля по ноябрь был осознанно упущен, но практика подсчета ничем не отличается от приведенных выше примеров. При сложении 12 показателей из правой колонки получится сумма кредита, которую необходимо будет вернуть в банк в течение года. Суммирование же третьей колонки позволит высчитать сумму переплаты, то есть той части, ради которой и работает кредитное учреждение.

Для расчета по аннуитетной формуле достаточно рассчитать процентную ставку по кредиту, так как сумму основного долга, необходимого к погашению ежемесячно мы уже знаем. Эта сумма равна 1000 рублей, поскольку такой способ платежа предполагает оплату равными долями.

(10000*(0,12/12))/(1–(1/(1/(1/ (0,12/12))))) = 833.

Следовательно, ежемесячно платить придется 1833 рубля.

Практика показывает, что дифференцированные кредиты гораздо выгоднее при долгосрочных займах, при которых в последние месяцы или годы выплаты уже не кажутся такими ощутимыми.

При низкой процентной ставке и малом сроке кредитования выбор можно сделать в пользу аннуитетного платежа, в котором самым проблемным станет не первый год, как при дифференцированном способе займа. Долговая нагрузка равномерно распределится между всеми периодами кредитования.

Расчет доли в процентах (удельного веса).

Давайте рассмотрим несколько примеров, которые помогут вам быстро вычислить долю в процентах от общей суммы в Excel для различных наборов данных.

Пример 1. Сумма находится в конце таблицы в определенной ячейке.

Очень распространенный сценарий — это когда у вас есть итог в одной ячейке в конце таблицы. В этом случае формула будет аналогична той, которую мы только что обсудили. С той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (со знаком $). Знак доллара фиксирует ссылку на итоговую ячейку, чтобы она не менялась при копировании формулы по столбцу.

Возьмем данные о продажах шоколада и рассчитаем долю (процент) каждого покупателя в общем итоге продаж. Мы можем использовать следующую формулу для вычисления процентов от общей суммы: 

=G2/$G$13

Вы используете относительную ссылку на ячейку для ячейки G2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца G. Но вы вводите $G$13 как абсолютную ссылку, потому что вы хотите оставить знаменатель фиксированным на G13, когда будете копировать формулу до строки 12.

Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.

На скриншоте ниже показаны результаты, возвращаемые формулой. Столбец «Процент к итогу» отформатирован с применением процентного формата.

Пример 2. Часть итоговой суммы находится в нескольких строках.

В приведенном выше примере предположим, что у вас в таблице есть несколько записей для одного и того же товара, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного товара.

В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному товару, а затем разделить это число на общую сумму заказов:

Учитывая, что столбец D содержит все наименования товаров, столбец F перечисляет соответствующие суммы, ячейка I1 содержит наименование, которое нас интересует, а общая сумма находится в ячейке F13, ваш расчет может выглядеть примерно так:

Естественно, вы можете указать название товара прямо в формуле, например:

Но это не совсем правильно, поскольку эту формулу придется часто корректировать. А это затратно по времени и чревато ошибками.

Если вы хотите узнать, какую часть общей суммы составляют несколько различных товаров, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на итоговую сумму. Например, по следующей формуле рассчитывается доля черного и супер черного шоколада:

Естественно, текстовые наименования товаров лучше заменить ссылками на соответствующие ячейки.

Для получения дополнительной информации о функции суммирования по условию ознакомьтесь со следующими руководствами:

• Как использовать функцию СУММЕСЛИ в Excel
• СУММЕСЛИМН и СУММЕСЛИ в Excel с несколькими критериями

Математическое объяснение

С точки зрения математики и ее основ решение задачи о том, как рассчитать процент от суммы, сводится только к применению простейших правил раскрытия скобок при умножении суммы на единое число и поиска общего знаменателя, который, в общем-то, им и является. Другими словами, представить в формульном выражении это можно так:

a x (b + c) = ab + ac ,

где ab и ac – произведения слагаемых в скобках (b и c) на число (коэффициент) перед скобками a.

Собственно, в пропорции действует тот же метод. Допустим, у нас есть некое число z, представляющее собой 100%, и сумма чисел a и b. Процент, который нужно вычислить, обозначим неизвестным числом y. В таком варианте пропорция принимает вид:

Отсюда простое решение:

((a + b) x 100%)/z = ((a x 100%) + (b x 100%))/z

В скобки действия взяты для того, чтобы подчеркнуть, что операции умножения выполняется в первую очередь, а сложение произведений – во вторую. Такое же действие производится, если изначально сумма чисел составляет 100%.

Как рассчитать общую сумму переплаты по кредиту

Стоит помнить, что итоговая сумма переплаты напрямую влияет на конечный остаток задолженности. Например, если заемщик будет регулярно вносить немного больше средств, чем расписано по графику платежей, то переплата также уменьшится. На сумму переплаты влияет и срок кредитования (чем он меньше, тем уменьшается величина переплат). Ног стоит понимать, что кредитные организации, оформляя ссуды, преследуют цель получения выгоды, поэтому отыскать банк, который кредитует население с нулевыми переплатами невозможно.

Формула простых процентов

Формула расчета простых процентов легко применима для просчета общей итоговой переплаты. Использовать ее может каждый потенциальный займополучатель. Для этого предварительно следует вооружиться следующими цифрами:

1. Использовать общую сумму ссуды. Например, 500 000.
2. Узнать стоимость одного процента: 500 000/100=5 000.
3. Перемножить величину процента на установленную ставку (допустим, размер годовых 18%): 5 000х18%=45 000 (годовая переплата).

Итоговый результат и становится показателем суммы переплаты. Если ссуда оформлена на несколько лет, то 45 000 следует умножить на их количество, чтобы высчитать общую переплату по всему периоду кредитования. Такая нехитрая формула начисления простых процентов поможет проанализировать предложения различных кредиторов и выбрать оптимальные под себя условия.

Расчет простых процентов

Расчет сложных процентов

Но не стоит забывать, что при оформлении займа, плательщик может столкнуться и с различными дополнительными взиманиями (за сборы, допуслуги, комиссионные, оформление и обслуживание ссуды). Такое встречается уже редко среди банков, но можно столкнуться и с такой процедурой кредитования. В данном случае при расчете полной переплаты следует учитывать и все дополнительные банковские сборы. Например, при годовой чистой переплате в 45 000, с учетом дополнительных взиманий (например, 2 500) переплата становится уже 47 500.

Расчет сложных процентов

Формула простых процентов по кредиту

Чтобы рассчитать конечную сумму долга вместе с процентами, обратимся к простым математическим вычислениям. Так, обозначим конечный размер займа «П»; первоначальную сумму кредита – А, % — величина процентной ставки, С – срок в днях, на который вы берет займ, а — %/100. СГ – количество дней в году, тогда:

П= А (1+а*С/СГ)

Пример:

Вы вязли ссуду на 10 000 грн. под 13% на 90 дней.

П= 10 000*(1+0,13*90/365) = 12 500 грн.

Таким образом, общая сумма, которую вам потребуется вернуть финансовому учреждению за 90 дней, равна 12 500 грн.

Как рассчитать кредит самостоятельно

Банк обязан предоставлять заемщику все сведения, связанные с выдачей кредита и с его исполнением. Это касается расчета полной стоимости кредита, помесячных платежей в графике. Но обращаться за расчетами в банк имеет смысл только после оформления договора и получения денег. Пока кредит не выдан, банк не связан с заемщиком договорными отношениями. Поэтому он может отказать в предоставлении расчетов и пояснений. В итоге для выбора и сравнения кредитных предложений такой вариант не подходит.

Онлайн-калькуляторы или ручной расчет

Все банки используют одинаковые формулы для расчета помесячных платежей. Естественно, делать такую работу вручную бессмысленно. Поэтому специалисты банка загружают исходные сведения в программы с формулами. Технические и математические ошибки в подсчетах встречаются крайне редко. В итоговых документах, которые получит заемщик, расчетные формулы не указываются.

Чтобы посчитать кредит самостоятельно, можно воспользоваться онлайн-калькуляторами в интернете, делать расчет вручную по формулам. В калькуляторы загружаются все исходные данные, от основной суммы долга и ставки процентов до размера дополнительных комиссий. В итоге калькулятор считает все сам, выдает вам результат по размерам ежемесячных платежей, сумма переплаты при разных условиях погашения кредита.

Формулы расчетов процентов по кредитам позволяют определить сумму ежемесячного платежа, общую переплату для заемщика
Расчеты можно сделать вручную или через интернет-калькуляторы. При этом формулы отличаются для аннуитетных и дифференцированных платежей

Вручную считать кредит очень сложно, особенно есть речь идет об аннуитетных платежах. Вам придется вникать в такие понятия как месячная и дневная процентная ставка, правильно подставлять все данные в формулы, перепроверять ручной расчет. Даже случайная ошибка в подсчетах или исходных данных может привести к неправильной оценке кредитного предложения, завысить или занизить размер переплаты.

По указанным причинам рекомендуем применять онлайн-калькуляторы. Их можно найти на сайтах кредитных организаций, на других интернет-ресурсах. Лучше перепроверять данные по нескольким калькуляторам, чтобы избежать ошибок. В этом случае вы сможете сделать объективное и обоснованное решение, выбрать оптимальные условия кредитования.

Какие данные нужны для расчета

Чтобы считать вручную или через онлайн-калькулятор, вам могут потребоваться следующие вводные данные:

• сумма кредита;
• точная ставка процентов;
• срок кредитования, количество платежей;
• дата начала платежей;
• сумма разовых комиссий, которые придется выплачивать заемщику;
• суммы ежемесячных комиссий.

В каждом онлайн-калькуляторе можно сразу указать, под какой вид платежей вы делаете расчет (дифференцированный или аннуитетный). Если вы считаете вручную, под каждый вид платежей нужно использовать разные формулы.

По дифференцированным платежам

Относительно просто рассчитать вручную проценты по дифференцированным платежам. Для этого нужно знать остаток долга по каждому ежемесячному платежу, ставку по кредиту. Формула для определения размера дифференцированных платежей:

Сп = (ООД х ПС х КДМ) / (100 х 365), где

Сп — сумма платежа
ООД — остаток по основному долгу
ПС — ставка в процентах годовых
КДМ — количество дней в месяце
(100 х 365) — произведение 100% на количество дней в году.

Формула используется для расчета каждого платежа отдельно, так как размер кредитного долга будет снижаться с каждым месяцем. После подсчета по всем платежам значения нужно суммировать. В итоге вы получите общую сумму переплаты под дифференцированные платежи.

Расчет делается с учетом того, что вы будете платить строго по графику, не планируете досрочно гасить кредит или нарушать сроки выплат. Если вы досрочно закроете часть кредита, остаток основного долга уменьшится. Следовательно, для определения суммы переплаты придется считать заново, подставляя уточненные показатели.

По аннуитетным платежам

Сделать расчет по аннуитетным платежам без онлайн-калькулятора намного сложнее. Вам придется применять формулу с многоуровневым делением, что непросто даже для профессионала в сфере финансов. Формула для определения размера аннуитетных платежей:

Сп = (СК х ПС / 12) / (1-(1 / 1 + ПС / 12) * (КП — 1)), где:

Сп — сумма платежа
СК — сумма кредита
ПС — ставка процентов годовых
КП — количество платежей по графику
* — показатель возведения в степень.

Сложно правильно посчитать все по этой формуле с первого раза. Чтобы избежать ошибок и быстро получить точные данные, лучше применять интернет-калькуляторы.

Заключение

Расходы по кредиту не ограничиваются только начисленными процентами.

При заключении кредита заемщику предлагается страховка, обычно в компании, имеющей связь с банком, иногда даже являющейся ее филиалом. Эта услуга предлагается добровольно-принудительной и может повлиять на получение одобрения от банка на выдачу кредита.

Кроме этого, имеется ряд дополнительных выплат, которые подразумевают оказание следующих услуг по этому кредиту:

• обслуживание счета;
• мобильный банкинг;
• ряд иных единовременных комиссий.

К возможным расходам можно также отнести штрафы и начисления за просроченные платежи – это может случиться, особенно если кредит долгосрочный.

Можно сказать, что простые проценты используются в случаях кредитов, где выплаты производятся аннуитетными платежами, которые менее выгодны клиенту. Поэтому, прежде чем брать кредит, следует реально оценить его потенциальную стоимость и взвесить все еще раз.