Подбор параметра в excel

Как пользоваться функциями подбора параметра и поиска решения в Excel

Функция поиска решения пригодится при необходимости определить неизвестную величину

Табличный процессор Microsoft Excel может выполнять не только простые операции с числами (сложение, умножение), расчет суммы или среднего значения. У этой программы имеется очень мощный функционал, который позволяет решать задачи разной сложности. Например, Эксель может оптимизировать значения в таблице, подставляя их таким образом, чтобы они удовлетворяли определенным критериям. Для этого программа оснащена специальными средствами для анализа данных: первый — это подбор параметра, а второй — поиск решения.

Чуть-чуть истории и теории.

Вы задумывались когда-нибудь — откуда и зачем в головах людей, живших в XVI…XVII веках, родились понятия дифференциалов, производных, интегралов? Объяснение, в общем-то, достаточно простое и понятное – эти ученые искали аналитические пути решения прикладных практических задач. И успешно находили!!!

Мне сегодня видится приблизительно такая «лестница» с качественными «ступенями инструментов» математики для решения практических и научных задач, которую изобрело человечество:

1. Арифметика — сложение, вычитание, умножение, деление.

2. Алгебра – применение элементарных функций (степенной, логарифмической, тригонометрической, …) и алгебраических уравнений функции одной переменной.

3. Гауссовские системы линейных уравнений.

4. Численные методы решения трансцендентных уравнений.

5. Численные методы решения систем трансцендентных уравнений функций нескольких переменных.

6. Дифференцирование и интегрирование функций одной переменной.

7. Дифференцирование и интегрирование функций нескольких переменных.

8. Системы дифференциальных и интегральных уравнений.

9. Масса разнообразных новых и старых специальных методик и подходов мне не известных и известных, но, безусловно, существующих и работающих.

Предлагаю остановиться и разобраться с достаточно высокой четвертой ступенью «лестницы».

Для численного решения нелинейных уравнений успешно применяются: метод половинного деления, метод простых итераций, метод хорд, метод касательных Ньютона, комбинированный метод секущих-хорд на основе итерационной формулы Ньютона. Для чего ученые-математики придумали множество различных методов решения трансцендентных уравнений? Они старались упростить и ускорить процесс расчетов. Надо помнить и понимать, что у них компьютеров не было, и расчеты выполнялись вручную.

Каждый из методов имеет свои достоинства и недостатки — они подробно описаны в литературе, и углубляться в них мы не будем. Скажу только, что из вышеперечисленных методов мне на практике довелось использовать все. При решении различных (в основном геометрических и теплотехнических) задач по разным причинам было удобно использовать то один, то другой подход. Метод Ньютона хорош своей быстрой сходимостью и простотой формулы. Комбинированный метод секущих-хорд на основе итерационной формулы Ньютона не требует нахождения производных, быстро «сходится», и главное – не требует анализа функции на сходимость. Метод половинного деления медленно сходится, но не требует никакого предварительного анализа функции.

Функция «Подбор параметра»

Подбор параметра в Excel позволяет подобрать какой-то определенный параметр, значение которого неизвестно. Чтобы было понятней, можно привести такой пример. Допустим, есть прямоугольник со сторонами A и B. Известно, что общая площадь этой фигуры составляет 400 квадратных метров, а сторона B — 40 метров. Сторона A неизвестна и, соответственно, нужно ее найти. Для решения такой задачи необходимо заполнить рабочий лист программы теми данными, которые уже известны. Для этого нужно создать таблицу с 2 колонками и 3 строками (диапазон ячеек A1:B3).

Первый столбец будет содержать название сторон прямоугольника и букву, обозначающую его площадь (т.е. A, B и S). А во втором столбце необходимо указать известные значения:

• в соседней ячейке для стороны B (ячейка B2) написать — 40 (значение для стороны А остается пустым);
• а в соседнем поле для площади прямоугольника (поле B3) написать следующую формулу: = B1*B2 (т.е. формула для расчета площади).

Если все было сделано правильно, то в поле B3 должно быть значение 0. Затем надо выделить эту ячейку и выбрать в панели меню пункты: «Сервис — Подбор параметра». В появившемся окне нужно указать то значение, которое должно быть получено в результате, т.е. 400. В строке «Установить в ячейке» будет указано поле «B3»: менять его не нужно, так и должно быть (сюда будет выведен результат). А в строке «Изменяя значение» необходимо выбрать неизвестный параметр, т.е. поле B1. После нажатия кнопки «ОК» программа выдаст результат: сторона А — 10 метров, а в поле общей площади прямоугольника будет указано число 400.

Это была очень простая задача на уровне 3 класса, но с помощью такой функции можно решать и более сложные задачи. Например, вы решили приобрести себе автомобиль в кредит. Вы точно знаете, что сможете выплачивать ежемесячную выплату в размере 1000 $ (но не больше), а также, что банк выдает автокредит с процентной ставкой 6,5%. Суть задачи заключается в следующем: «Какова максимальная сумма машины, которую можно взять в кредит на таких условиях?». То есть теперь программа будет искать стоимость автомобиля, отталкиваясь от того, что ежемесячный платеж не должен превышать 1000 $. Такой пример является уже более сложным, а также более практичным, нежели расчет площади прямоугольника.

Подбор параметра в EXCEL

Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра .

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным .

4 комментариев

Добрый день, Александр!

Есть задача которую я не могу понять с помощью какой формулы описать решение, причем прописать эти формулы в гугл таблице, но думаю суть та же будет если сделать это и в эксели если в кратце: то например я знаю что мне надо накопить 20000, то если откладывать каждый месяц по 10 000 то через 2 месяца я добъюсь цели, как это описать формульно чтобы эксель показал что в зависимости от того сколько накапливается в месяц я смогу накопить 20000? чтобы программа показала мне время через которое я накоплю средства есть столбец месяцев с суммами того что накопил в этих столбцах при этом там есть и пустыми суммы за декабрь например. Просто бьюсь уже 5 дней не могу понять возможно ли решение для такой задачи или нет. ссылка на файл о чем речь : https://docs.google.com/spreadsheets/d/1kyP2HwB8WFeAqJkkANC9TxQCsIv3K-44Wfe3xabfQeA/edit?usp=sharing

Даниил, здравствуйте. Уточните пожалуйста вопрос.Вы хотите, чтобы программа считала срок исходя из какого-то обязательного ежемесячного платежа, или из средних ежемесячных накоплений за какой-то период?

Исходя из средних ежемесячных накоплений( суммы которых могут быть разными за месяцы) за какой либо период времени

Даниил, в Excel есть функция, которая считает средние значения — СРЗНАЧ. Тогда формула расчета количества месяцев будет такая: =/СРЗНАЧ). Естественно, в фигурных скобках я указал описания, а вы укажите соответствующие ссылки на ячейки и диапазоны ячеек

Инструмент «Поиск решения»

Как Вы убедились, подбор параметра отлично и безотказно работает практически во всех случаях. Но у него есть недостаток – он манипулирует лишь одним значением для изменения результата. А что, если нужно построить более сложную систему вычислений? Тогда используем «Поиск решения».

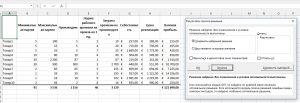
И снова рассмотрим на примере. Спланируем производственный процесс на месяц для получения максимальной прибыли. Вот наша таблица заготовка:

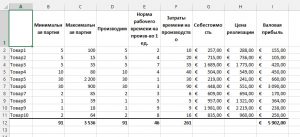
В таблице имеем такие поля:

1. Минимальная партия – минимальное количество товара, которое нужно произвести для обслуживания уже существующих заказов;
2. Максимальная партия – наибольшее количество товара, которое можно произвести, исходя из запасов сырья
3. Норма рабочего времени – количество человекочасов, необходимых для производства одного изделия;
4. Затраты рабочего времени – количество времени, которое будет затрачено на производство всего запланированного. Пусть у нас работает 20 работников по 8 часов 22 дня в месяце. Тогда сумма по этому полю должна составить 3520 ч.
5. Себестоимость – стоимость производства одной единицы продукции
6. Цена реализации – рыночная стоимость одной единицы продукции
7. Валовая прибыль – прибыль, которая будет получена от реализации изготовленного товара.

Для упрощения, будем считать, что спрос на товар выше производственных возможностей, и всё произведенное будет продано. Так сколько чего нам нужно произвести, чтобы получить наибольшую выгоду, а персонал трудился ровно 3520 ч? Запускаем «Поиск решения»:

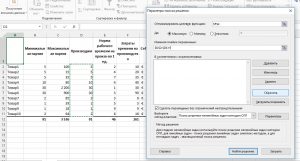
1. Ищем на ленте Данные – Анализ – Поиск решения . Кликаем, откроется окно настройки;
2. В поле «Оптимизировать целевую функцию» задаем ссылку на сумму по столбцу «Валовая прибыль»;
3. В поле «До» выбираем «Максимум». В других случаях можно выбрать «минимум», или задать какое-то конкретное значение;
4. В списке «Изменяя ячейки переменных» указываем все строки столбца «Производим»
5. Далее нужно внести все оговоренные выше ограничения. Для этого жмем «Добавить» и в открывшемся окне выбираем ссылки на ячейки и параметры их ограничения:

Вносим все оговоренные ограничения, они отобразятся в списке окна настройки:

1. Суммарные затраты времени должны равняться 3520 часов;
2. Производимое количество больше или равно минимальной партии
3. Производимое количество меньше или равно максимальной партии
4. Производимое количество должно быть целым числом

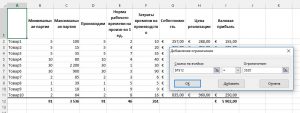
1. Выбираем метод решения в соответствии с рекомендациями разработчиков внизу окна настроек. Мы выберем линейный метод. Жмем «Найти решение», по завершению поиска программа сообщает о результате.

В этом окне можно подтвердить внесение изменений в ячейки, либо вернуться к изначальному набору данных. Так же, отличным решением будет сохранить результаты поиска как сценарий . Позднее их можно будет восстановить и построить соответствующие отчеты.

Видим, что программа оптимизировала наши производственные процессы и направила в русло получения максимальной прибыли. При этом, у нас не будет переработок и недоработок. Таки образом, можно решать многие задачи планирования и проектирования бизнес-процессов.

Экспериментируя с многочисленными настройками инструмента, можно детально управлять процессом поиска. На самом деле, «Поиск решения» — очень функциональная и многогранная надстройка, познать все азы которой можно на сайте разработчика: www.solver.com.

Кстати, если Вы не нашли на ленте этот инструмент – не отчаивайтесь, его просто нужно подключить. Для этого нажмите Файл – Параметры – Надстройки . Внизу в раскрывающемся списке «Управление» выберите «Надстройки Excel» и нажмите «Перейти». В открывшемся окне поставьте галку напротив «Поиск решения» и нажмите Ок. Вот и всё, он сразу же появится ленте!

Вот такие существуют способы подгонки результатов, о которых мало кто знает и мало кто пользуется. Тем не менее, навыки работы с ними делают нашу жизнь проще, теперь не нужно вручную перебирать десятки или сотни значений, чтобы получить нужный результат!

Экспериментируйте, а я отправляюсь писать следующий пост. До новых встреч на страницах блога officelegko.com!

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым – изменяемые ячейки.

Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Трансцендентные уравнения. Два метода решения в Excel.

Если у вас на компьютере нет программы MS Excel, то расчеты можно выполнить в программе OOo Calc из бесплатного пакета Open Office.

Задач, которые требуют для получения ответа составления и решения трансцендентных уравнений, вокруг нас очень много. Это — задачи и физики, и теплотехники, и астрономии, и элементарной геометрии в обычной жизни… Инженерам-конструкторам и программистам в повседневной работе необходимо уметь составлять и быстро решать численными методами нелинейные уравнения. На мой взгляд — это один из критериев профессионализма. Более того, уравнения, которые решаются аналитически, сегодня иногда гораздо проще и быстрее при наличии вычислительной техники решить численными методами, поэтому нужно уметь это делать.

Вычисление угла зацепления зубчатой передачи методом Ньютона (методом касательных)

Рассмотрим пример из статьи «Расчет геометрии зубчатой передачи». Необходимо найти угол зацепления зубчатой передачи atw. Я обещал в той статье рассказать, как это делается. Выполняю обещание.

Если расстояние между центрами колеса и шестерни не задано, то угол зацепления  можно вычислить путем решения трансцендентного уравнения:

inv (atw)=tg (atw) —atw=2*xs*tg (a)/(z2+T*z1)+tg (at) —at

Подставив данные из примера, рассмотренного в вышеупомянутой статье, получим после преобразований следующее уравнение:

inv (atw)=0,020910

f (atw)=tg (atw)—atw-0,020910=0

Используем метод Ньютона, потому что взять производную представленной выше функции элементарно просто, а итерационная формула очень проста и компактна:

f’(atw)=1/(cos (atw))^2—1

atw(i+1)= atwi— f (atw) i/ f’(atw) i

Открываем файл Excel и начинаем работу.

Исходные данные  будем традиционно писать в ячейки со светло-бирюзовой заливкой. Результаты расчетов будем считывать в ячейках со светло-желтой заливкой.

1. Инволюту угла зацепления inv(atw) заносим

в ячейку D3: 0,020910

2.Значение угла зацепления в нулевом приближении atwв радианах записываем

в D4: =ПИ()/4

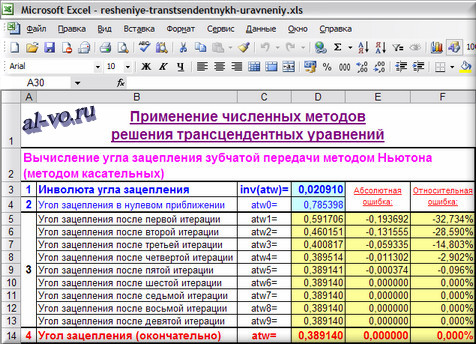
3.Итерационную формулу atw(i+1)= atwi— f(atw)if’(atw)i заносим

в D5: =D4- (TAN (D4) -D4-$D$3)/(1/(COS (D4))^2-1)=0,591706

atw1= atw0- (tg (atw0) — atw0- inv (atw))/(1/(cos (atw0))^2-1)

и копируем в ячейки D6… D14

4.Видим, что уже после шестой итерации угол зацепления atw в радианах вычислен с нулевой абсолютной и относительной ошибкой:

atw =D13- (TAN (D13) -D13-$D$3)/(1/(COS (D13))^2-1)=0,389140

Решение найдено, расчет в Excel завершен!

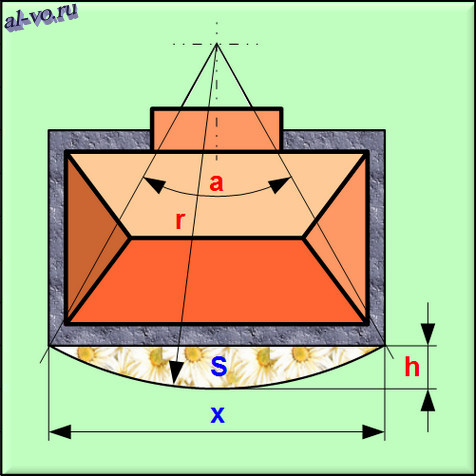
Решение задачи ландшафтного дизайна с помощью сервиса  «Подбор параметра» в Excel

Задача:

Вдоль отмостки стены дома длиной 14 метров необходимо разбить цветник в виде сегмента круга площадью ровно 16 квадратных метров. На сколько метров цветник будет отстоять от края отмостки по центру стены? Каким радиусом необходимо выполнить границу цветника?

1. Длину отмостки стены дома — хорды сегмента круга x в метрах записываем

в ячейку D17: 14,000

2.Площадь цветника – сегмента круга Sв квадратных метрах вписываем

в D18: 16,000

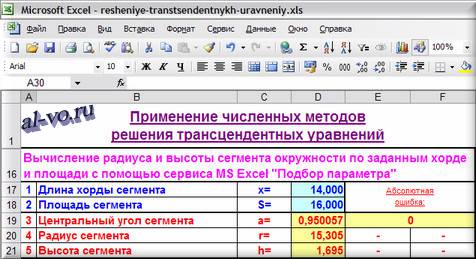
3. Предположительное произвольное (не нулевое) значение центрального угла сегмента aв радианах пишем

в D19: 1,000

Трансцендентное уравнение  asin(a/2) -2*cos (a/2) — (8*S/x^2) *sin(a/2)=0 вводим

в объединенную ячейку E19F19: =D19/SIN (D19/2) -2*COS (D19/2) — (8*D18/D17^2)*SIN (D19/2)

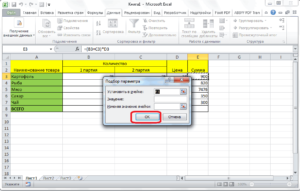
Включаем сервис «Подбор параметра» в Excel: «Сервис» – «Подбор параметра». Пишем в появившемся окне все как на рисунке слева и нажимаем кнопку OK.

В появившемся новом окне видим, что решение найдено, снова нажимаем на кнопку OK.

_

Считываем искомое значение центрального угла сегмента a в радианах

в D19:  0,950057

При этом видим, что значение трансцендентного уравнения равно нулю; считываем

в объединенной ячейке E19F19: =D19/SIN (D19/2) -2*COS (D19/2) — (8*D18/D17^2)*SIN (D19/2)=0

4. Радиус наружной границы цветника – радиус сегмента круга rв метрахрассчитывается

в D20: =D17/2/SIN (D19/2)=15,305

r=x/2sin(a/2)

5. Максимальная ширина цветника – высота сегмента круга hв метрахрассчитывается

в ячейке D21: =D20*(1-COS (D19/2))=1.695

h=r*(1- cos(a/2))

Ответы получены, вторая задача успешно решена!

Я не приводил вывода использованных формул потому, что это не по теме поста, и, думаю, с геометрией и тригонометрией вы легко разберетесь. Будут вопросы – обращайтесь.

Чтобы получать информацию о выходе новых статей вам нужно подписаться на анонсы в окне, расположенном вверху страницы. Введите адрес своей электронной почты и нажмите на кнопку «Получать анонсы статей». С этого момента к вам на почтовый ящик будет приходить небольшое уведомление о появлении на моем блоге новой статьи.

Решение уравнения с помощью подбора параметров

Для примера воспользуемся простым уравнением без степеней и корней, чтобы можно было наглядно посмотреть, как производится решение.

1. У нас есть уравнение: х+16=32. Необходимо понять, какое число прячется за неизвестным «х». Соответственно, будем находить его с помощью функции «Подбор параметра». Для начала прописываем в ячейку наше уравнение, предварительно поставив знак «=». Причем вместо «х» устанавливаем адрес ячейки, в которой появится неизвестное. В конце введенной формулы знак равенства не ставим, иначе у нас отобразиться «ЛОЖЬ» в ячейке.
2. Переходим к запуску функции. Для этого действуем аналогичным образом, как и в предшествующем способе: во вкладке «Данные» находим блок «Прогноз». Здесь кликаем на функции «Анализ, что, если», а затем переходим к инструменту «Подбор параметра».
3. В появившемся окне в поле «Установить значение» прописываем адрес той ячейки, в которой у нас указано уравнение. То есть это окошко «К22». В поле «Значение», в свою очередь, прописываем число, которому равно уравнение – 32. В поле «Изменяя значение ячейки» вводим адрес, куда будет вписываться неизвестное. Подтверждаем свое действие нажатием на кнопку «ОК».
4. После нажатия на кнопку «ОК» появится новое окно, в котором четко прописано, что значение для заданного примера найдено. Выглядит это следующим образом:

Во всех случаях, когда производится вычисление неизвестных путем «Подбора параметров», должна бы установлена формула, без нее найти численное значение невозможно.

В статье мы разобрали для варианта использования функции «Подбор параметра». Но обратите внимание на то, что в случае с нахождением неизвестного можно пользоваться инструментом при условии, что имеется только одно неизвестное. В случае же с таблицами подбирать параметры нужно будет индивидуально для каждой ячейки, так как опция не приспособлена работать с целым диапазоном данных

Подбор параметра в MS EXCEL

Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8).

Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5).

 Подбирать параметр вручную – скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра.

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным.

Простейший пример

Найдем значение параметра b в уравнении 2*а+3*b=x, при котором x=21, параметр а=3.

Подготовим исходные данные.

Значения параметров а и b введены в ячейках B8 и B9. В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x). Целевое значение x в ячейке B11 введенодля информации.

Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…).

В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b).

Нажмите ОК.

Инструмент Подбор параметра подобрал значение параметра b равное 5.

Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно.

Примечание: Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b, которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан).

Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения).

Решим квадратное уравнение x2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.

к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший.

Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X – аналитический. Решение b=(X-2*a)/3) очевидно.

Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).

Калькуляция, подбираем значение прибыли

Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (С8), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (С14) равно 0.

В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль (=С7+С8). Стоимость договора (ячейка С11) вычисляется как Цена продукции + НДС (=СУММ(С9:C10)).

Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент Подбор параметра.

Нажмите ОК.

Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.

3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

СУММЕСЛИМН

Функция СУММЕСЛИМН позволяет суммировать значения по определенным условиям. Условий может быть несколько. В Excel также есть функция СУММЕСЛИ, которая позволяет суммировать по одному критерию. Призываю вас использовать более универсальную формулу.

У функции СУММЕСЛИМН следующий синтаксис:

— Диапазон суммирования — область листа Эксель, из которой мы суммируем данные- Диапазон условия 1 — Диапазон ячеек, которые мы проверяем на соответствие условию- Условие 1 — Условие, которое проверяется на соответствие в Диапазоне 1.Обратите внимание, что диапазонов условий и соответственно условий может быть столько, сколько вам нужно. Для примера выше мы хотим получит выручку, которую принес нам Петров в городе Москва

Формула имеет вид СУММЕСЛИМН(C2:C13;A2:A13;E2;B2:B13;F2), где C2:C13 — диапазон со значениями выручки, которые необходимо просуммировать; А2:А13 — диапазон с фамилиями, которые мы будем проверять; Е2 — ссылка на конкретную фамилию; B2:B13 — ссылка на диапазон с городами; F2 — ссылка на конкретный город

Для примера выше мы хотим получит выручку, которую принес нам Петров в городе Москва. Формула имеет вид СУММЕСЛИМН(C2:C13;A2:A13;E2;B2:B13;F2), где C2:C13 — диапазон со значениями выручки, которые необходимо просуммировать; А2:А13 — диапазон с фамилиями, которые мы будем проверять; Е2 — ссылка на конкретную фамилию; B2:B13 — ссылка на диапазон с городами; F2 — ссылка на конкретный город.

Более подробно о функциях СУММЕСЛИМН и СУММЕСЛИ рассказано в статье «СУММЕСЛИ и СУММЕСЛИМН в Excel».

Функции программы Microsoft Excel: подбор параметра

Очень полезной функцией в программе Microsoft Excel является Подбор параметра. Но, далеко не каждый пользователь знает о возможностях данного инструмента. С его помощью, можно подобрать исходное значение, отталкиваясь от конечного результата, которого нужно достичь. Давайте выясним, как можно использовать функцию подбора параметра в Microsoft Excel.

Скачать последнюю версию Excel

• Суть функции
• Применение функции на практике
• Решение уравнений

Суть функции

Если упрощенно говорить о сути функции Подбор параметра, то она заключается в том, что пользователь, может вычислить необходимые исходные данные для достижения конкретного результата. Эта функция похожа на инструмент Поиск решения, но является более упрощенным вариантом.

Её можно использовать только в одиночных формулах, то есть для вычисления в каждой отдельной ячейке нужно запускать всякий раз данный инструмент заново.

Кроме того, функция подбора параметра может оперировать только одним вводным, и одним искомым значением, что говорит о ней, как об инструменте с ограниченным функционалом.

Применение функции на практике

Для того, чтобы понять, как работает данная функция, лучше всего объяснить её суть на практическом примере. Мы будем объяснять работу инструмента на примере программы Microsoft Excel 2010, но алгоритм действий практически идентичен и в более поздних версиях этой программы, и в версии 2007 года.

Имеем таблицу выплат заработной платы и премии работникам предприятия. Известны только премии работников. Например, премия одного из них — Николаева А. Д, составляет 6035,68 рублей. Также, известно, что премия рассчитывается путем умножения заработной платы на коэффициент 0,28. Нам предстоит найти заработную плату работников.

Для того, чтобы запустить функцию, находясь во вкладке «Данные», жмем на кнопку «Анализ «что если»», которая расположена в блоке инструментов «Работа с данными» на ленте. Появляется меню, в котором нужно выбрать пункт «Подбор параметра…».

После этого, открывается окно подбора параметра. В поле «Установить в ячейке» нужно указать ее адрес, содержащей известные нам конечные данные, под которые мы будем подгонять расчет.

В данном случае, это ячейка, где установлена премия работника Николаева. Адрес можно указать вручную, вбив его координаты в соответствующее поле.

Если вы затрудняетесь, это сделать, или считаете неудобным, то просто кликните по нужной ячейке, и адрес будет вписан в поле.

В поле «Значение» требуется указать конкретное значение премии. В нашем случае, это будет 6035,68. В поле «Изменяя значения ячейки» вписываем ее адрес, содержащей исходные данные, которые нам нужно рассчитать, то есть сумму зарплаты работника. Это можно сделать теми же способами, о которых мы говорили выше: вбить координаты вручную, или кликнуть по соответствующей ячейке.

Когда все данные окна параметров заполнены, жмем на кнопку «OK».

Подобную операцию можно проделать и для других строк таблицы, если известна величина премии остальных сотрудников предприятия.

Решение уравнений

Кроме того, хотя это и не является профильной возможностью данной функции, её можно использовать для решения уравнений. Правда, инструмент подбора параметра можно с успехом использовать только относительно уравнений с одним неизвестным.

Допустим, имеем уравнение: 15x+18x=46. Записываем его левую часть, как формулу, в одну из ячеек. Как и для любой формулы в Экселе, перед уравнением ставим знак «=». Но, при этом, вместо знака x устанавливаем адрес ячейки, куда будет выводиться результат искомого значения.

В нашем случае, формулу мы запишем в C2, а искомое значение будет выводиться в B2. Таким образом, запись в ячейке C2 будет иметь следующий вид: «=15*B2+18*B2».

Запускаем функцию тем же способом, как было описано выше, то есть, нажав на кнопку «Анализ «что если»» на ленте», и перейдя по пункту «Подбор параметра…».

В открывшемся окне подбора параметра, в поле «Установить в ячейке» указываем адрес, по которому мы записали уравнение (C2).

В поле «Значение» вписываем число 45, так как мы помним, что уравнение выглядит следующим образом: 15x+18x=46.

В поле «Изменяя значения ячейки» мы указываем адрес, куда будет выводиться значение x, то есть, собственно, решение уравнения (B2). После того, как мы ввели эти данные, жмем на кнопку «OK».

Как видим, программа Microsoft Excel успешно решила уравнение. Значение x будет равно 1,39 в периоде.

Изучив инструмент Подбор параметра, мы выяснили, что это довольно простая, но вместе с тем полезная и удобная функция для поиска неизвестного числа. Её можно использовать как для табличных вычислений, так и для решения уравнений с одним неизвестным.