Округление чисел — правила и примеры решения для 5 класса

Общий порядок округления и терминология

• Округление числа, записанного в позиционной системе счисления с M знаками дробной части, может производиться «до K-го знака после запятой», где K ≤ M. При таком округлении в записи числа отбрасываются справа (M-K) значащих цифр, а K-я цифра после запятой может измениться. Применяется также терминология с указанием единицы наименьшей десятичной доли, сохраняющейся у округлённого числа, то есть «округление до десятых», «…до сотых», «…до тысячных» и т. д. (соответствует округлению до одного, двух, трёх и так далее знаков после запятой). Частный случай, когда K=0, называется «округлением до целого».
• Когда при округлении отбрасываются значащие цифры целой части числа, говорят об «округлении до десятков» (сотен, тысяч и так далее), отбрасывая, соответственно, один, два, три и более знака. При таком округлении отбрасываемые цифры целой части числа заменяются на нули.
• Для чисел, представленных в нормализованном виде, говорят об «округлении до K (значащих) цифр». При этом мантисса числа сохраняет K значащих цифр, остальные цифры справа отбрасываются.

Правила округления

Коммерческое округление

В Коммерческие туры (не отрицательные числа) выглядит следующим образом :

• Если число в первом десятичном разряде равно 0, 1, 2, 3 или 4, оно округляется в меньшую сторону.
• Если число в первом десятичном разряде — 5, 6, 7, 8 или 9, то оно округляется в большую сторону.

Это правило округления описано в стандарте DIN 1333 . Округление часто уже преподается в начальной школе.

Примеры (округление до двух знаков после запятой):

• 13,3749 … € ≈ 13,37 €
• 13,3750 … € ≈ 13,38 €

Отрицательные числа в зависимости от их величины округлой формы, на 5 , чтобы сказать от нуля ( Engl : от нуля ):

• −13,3749 … € ≈ −13,37 €
• −13,3750 … € ≈ −13,38 €

В Коммерческих турах частично в правовой среде , как гражданские раунды , называемых и г. Б. в о поставщиках государственных услуг пояснил следующее:

Симметричное закругление

Коммерческое и симметричное округление отличаются друг от друга только тем, что число округляется точно посередине между двумя числами с выбранным количеством десятичных цифр.

Симметричные (или геодезическим, математический, искажаются, научный ) округление определяются следующим образом (композиция адаптирована):

1. Если число в первом десятичном разряде равно 0, 1, 2, 3 или 4, оно округляется в меньшую сторону.
2. Если цифра 5 (за которой следуют другие цифры, которые не все равны нулю), 6, 7, 8 или 9 в первом десятичном разряде, она округляется в большую сторону.
3. Если число в первом десятичном разряде — только 5 (или 5, за которой следуют только нули), оно округляется таким образом, чтобы последнее сохраняемое число было четным («правило четных чисел»).

Этот тип округления используется в числовой математике , инженерии и технике. Он предусмотрен стандартом IEEE 754 для вычислений с двоичными числами с плавающей запятой в компьютерах. В англоязычной литературе это называется Round to Even или Banker’s Rounding .

Примеры (округление до одного десятичного знака):

• 2,2499 ≈ 2,2 (по правилу 1)
• 2,2501 ≈ 2,3 (по правилу 2)
• 2,2500 ≈ 2,2 (округлено до четного числа согласно правилу 3)
• 2,3500 ≈ 2,4 (округлено до четного числа согласно правилу 3)

Коммерческое округление, описанное в предыдущем разделе, создает небольшие систематические ошибки, поскольку округление на 0,5 происходит в большую сторону, а в меньшую сторону на 0,5 никогда не происходит; это может немного исказить статистику. Описанное здесь математическое округление всегда округляется в большую или меньшую сторону от точной середины между двумя цифрами до следующей четной цифры. В результате среднее значение округляется в сторону увеличения и уменьшения примерно так же часто, по крайней мере, если исходные числа являются стохастическими . (Контрпример: если маленькие числа встречаются чаще, чем большие, их можно систематически округлять в меньшую сторону, а не в большую, см . Закон Бенфорда .)

Округление с сохранением суммы

При округлении с сохранением суммы слагаемые округляются таким образом, чтобы их сумма была равна округленной сумме слагаемых. Может потребоваться округлить некоторые слагаемые от ближайшего округленного значения до противоположного значения.

Важными приложениями являются пропорциональное распределение мест и распределение всего НДС в счете-фактуре по его отдельным позициям.

Случай, когда все слагаемые положительные, был тщательно исследован, см. Процедуру распределения мест .

Метод Хара-Нимейера может быть обобщен для слагаемых с обоими знаками : вы округляете все числа до ближайших круглых чисел, и пока сумма слишком велика (или слишком мала), вы выбираете одно из округленных (или округленных) чисел. ) нумерует с наибольшим округление (или самое большое количество округления вниз) и изменяет его округления в направлении , противоположном. Это означает, что сумма сумм изменений минимальна .

Методы

В разных сферах могут применяться различные методы округления. Во всех этих методах «лишние» знаки обнуляют (отбрасывают), а предшествующий им знак корректируется по какому-либо правилу.

• Округление к ближайшему целому — наиболее часто используемое округление, при котором число округляется до целого, модуль разности с которым у этого числа минимален. В общем случае, когда число в десятичной системе округляют до N-го знака, правило может быть сформулировано следующим образом:
  • если N+1 знак < 5, то N-й знак сохраняют, а N+1 и все последующие обнуляют;
  • если N+1 знак ≥ 5, то N-й знак увеличивают на единицу, а N+1 и все последующие обнуляют;

  Например: 11,9 → 12; −0,9 → −1; −1,1 → −1; 2,5 → 3.

  Максимальная дополнительная абсолютная погрешность, вносимая при таком округлении (погрешность округления), составляет ±0,5 последнего сохраняемого разряда.

• Округление к большему (округление к +∞, округление вверх, англ. ceiling — досл. «потолок») — если обнуляемые знаки не равны нулю, предшествующий знак увеличивают на единицу, если число положительное, или сохраняют, если число отрицательное. В экономическом жаргоне — округление в пользу продавца, кредитора (лица, получающего деньги). В частности, 2,6 → 3, −2,6 → −2. Погрешность округления — в пределах +1 последнего сохраняемого разряда.
• Округление к меньшему (округление к −∞, округление вниз, англ. floor — досл. «пол») — если обнуляемые знаки не равны нулю, предшествующий знак сохраняют, если число положительное, или увеличивают на единицу, если число отрицательное. В экономическом жаргоне — округление в пользу покупателя, дебитора (лица, отдающего деньги). Здесь 2,6 → 2, −2,6 → −3. Погрешность округления — в пределах −1 последнего сохраняемого разряда.
• Округление к большему по модулю (округление к бесконечности, округление от нуля) — относительно редко используемая форма округления. Если обнуляемые знаки не равны нулю, предшествующий знак увеличивают на единицу. Погрешность округления составляет +1 последнего разряда для положительных и −1 последнего разряда для отрицательных чисел.
• Округление к меньшему по модулю (округление к нулю, целое англ. fix, truncate, integer) — самое «простое» округление, поскольку после обнуления «лишних» знаков предшествующий знак сохраняют, то есть технически оно состоит в отбрасывании лишних знаков. Например, 11,9 → 11; −0,9 → 0; −1,1 → −1). При таком округлении может вноситься погрешность в пределах единицы последнего сохраняемого разряда, причём в положительной части числовой оси погрешность всегда отрицательна, а в отрицательной — положительна.
• Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, при этом вероятность округления вверх равна дробной части. Этот способ делает накопление ошибок случайной величиной с нулевым математическим ожиданием.

Способы округления чисел

Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.

Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .

math.ceil() — округление чисел в большую сторону

Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.

Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.

Пример:

math.ceil(5.15) # = 6
math.ceil(6.666) # = 7
math.ceil(5) # = 5

Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.

math.floor() — округление чисел в меньшую сторону

Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.

Пример:

math.floor(7.9) # = 7
math.floor(9.999) # = 9
math.floor(-6.1) # = -7

math.trunc() — отбрасывание дробной части

Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.

Примеры:

math.trunc(5.51) # = 5
math.trunc(-6.99) # = -6

Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .

Примеры:

int(5.51) # = 5
int(-6.99) # = -6

Нормальное округление

Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.

И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().

Примеры:

math.floor(9.999) # = 9
int(9.999) # = 9
math.ceil(-9.999) # = -9
int(-9.999) # = -9

Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.

Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:

def int_r(num):
    num = int(num + (0.5 if num > 0 else -0.5))
    return num

Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).

Примеры:

int_r(11.5) # = 12
int_r(11.4) # = 11
int_r(-0.991) # = -1
int_r(1.391) # = 1

round() — округление чисел

round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.

В Python 2

Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.

Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».

Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.

В Python 3

В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.

Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.

Примеры:

round(3.5) # = 4
round(9.5) # = 10
round(6.5) # = 6
round(-6.5) # = -6
round(-7.5) # = -8

Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.

Округление до сотых

У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.

Пример округления до нужного знака:

round(3.555, 2) # = 3.56
round(9.515,1) # = 9.5
round(6.657,2) # = 6.66

Округление в Excel — это просто!

​Финансовый​ целого (77)​Павел кольцов​Статистические. «БЕТАОБР»​

​ разрядов, которое в​ Каждая клетка такой​ конкретной цифры​ 10​ число округляется слева​Функция «ОТБР»​Округление до сотен в​

​ формата ячейки одну​ математики, цифра 5​ числа.​в ячейке, то​ Она работает точно​

​800​,​=ОКРУГЛВВЕРХ (3,14159; 3)​: тогда уж до​- делает возврат​ ней помещается для​

​ таблицы называется ячейкой.​.​0​ от запятой.​–​ Excel​

​ цифру после запятой.​

​ после запятой округляется​На вкладке​

​ значение будет равно​ так же, как​Число 800 ближе к​

1. ​Процентный​ Округляет с избытком​ десятков. =округл (…/10;0)*10.​ обратной функции к​ видимости пользователя. Но​Ячейка Excel имеет свой​Для того, чтобы​=ОКРУГЛ(-50,55;-2)​Чтобы округление всегда выполнялось​
2. ​округляет до целого числа,​по такой формуле​Как правильно написать в​ в большую сторону.​Главная​ 283000.​ функция ОКРУГЛ, за​ 823,7825, чем к​или​ число 3,14159 до​ вместо точек то,​ интегральной функции плотности​ в этом случае​
3. ​ индивидуальный адрес, состоящий​ установить цену по​Округляет число -50,55 до​ в большую по​ отбрасывая все цифры​ =ОКРВВЕРХ(C15;100), т.д.​

​ строке «Число_разрядов»​

​ Чем больше цифр​в группе​Нажмите кнопку​ исключением того, что​ 900. Наверное, теперь​Экспоненциальный​ трех десятичных разрядов​​ что нужно округлить.​ бета-вероятности.​ округления как такового​ из номера строки​ скидке не ниже​ ближайшего числа, кратного​ модулю сторону, используйте​ после запятой.​Другие способы округления​

​.​ после запятой, тем​Буфер обмена​ОК​ она всегда округляет​ вам все понятно.​в зависимости от​ (3,142)​ наверное так​«ВЕЙБУЛЛ»​ не происходит. При​ и латинской буквы​ цены себестоимости, можно​ 100​ функцию​Бывает, нужно​

​ вверх, до определенной​Если поставим цифру​ точнее считает.​нажмите кнопку​

​.​​ число в меньшую​Чтобы округлить до ближайших​ типа ваших данных.​=ОКРУГЛВВЕРХ (-3,14159; 1)​Александр смольников​- возврат распределения​

​ изменении размера ячейки,​​ столбца (например, 1А,​ применить такую формулу.​-100​ОКРУГЛВВЕРХ​округлить числа в Excel​ цифры, т.д., смотрите​ 1, то после​Здесь оставили две цифры​

​Копировать​​В строке состояния будет​ сторону. Например, необходимо​десятков​

​В поле​​ Округляет с избытком​: Округляет число до​ Вейбулла.​ количество разрядов также​ 2В, 5С).​=МАКС(ОКРВВЕРХ(СУММ(C2*0,9);1);B2)​Округление в Excel​.​ до кратного числа​ в статье «Округление​ запятой будет стоять​ после запятой (форматом​(или нажмите клавиши​ отображаться индикатор​ округлить число 3,14159​Введите​

​Число десятичных знаков​​ число -3,14159 до​ ближайшего большего по​

​Также MS Office Excel​​ изменяется как в​Основные функции программы​

​Копируем формулу вниз​можно проводить не​

​Чтобы округление всегда выполнялось​​. Например, чтобы все​ Excel в большую​ одна цифра.​ ячейки). Получилось так.​​ CTRL+C).​​Фиксированный десятичный формат​ до трех разрядов:​

​=ОКРУГЛ(A1;-1)​введите число знаков​​ одного десятичного разряда​​ модулю.​​ имеет​​ большую, при увеличении​​Функция «СУММ» (сумма в​ по столбцу. Получилось​

​ только по правилам​ до ближайшего меньшего​ числа делились на​ сторону».​Если поставим цифру​Здесь мы убрали в​Выделите на листе ячейки,​

​.​

fb.ru>

Как будет округлено число в зависимости от того, что мы укажем в “числе разрядов”?

• Если число_разрядов больше 0, то число округляется до указанного количества дробных разрядов.
• Если число_разрядов равно 0, то число округляется до ближайшего целого.
• Если число_разрядов меньше 0, то число округляется слева от запятой.

Примеры:

Примеры округлений.

Также существуют функции направленного округления

• Чтобы округление всегда выполнялось в большую по модулю сторону, используйте функцию ОКРУГЛВВЕРХ.
• Чтобы округление всегда выполнялось до ближайшего меньшего по модулю, используйте функцию ОКРУГЛВНИЗ.
• Чтобы число округлялось с нужной кратностью (например, до ближайшего числа, кратного 0,5), используйте функцию ОКРУГЛТ.

Использование округлений при работе с числами ограниченной точности

Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного истинного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах ошибки измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.

Получение приближенных значений

Это математическое действие осуществляется по определенным правилам.

Но для каждого множества чисел они разные. Отмечают, что округлить можно целые числа и десятичные дроби.

А вот с обыкновенными дробями действие не выполняется.

Сначала их необходимо перевести в десятичные дроби, а затем приступить к процедуре в необходимом контексте.

Правила приближения значений заключаются в следующем:

• для целых – замена разрядов, следующих за округляемым, нулями,
• для десятичных дробей – отбрасывания всех чисел, которые находятся за округляемым разрядом.

К примеру, округляя 303 434 до тысяч, необходимо заменить сотни, десятки и единицы нулями, то есть 303 000. В десятичных дробях 3,3333 округляя до десятых, просто отбрасывают все последующие цифры и получают результат 3,3.

32 Comments

Не правильная теория про если цифра 46.5 это не 47 а 46 это называется еще банковским округлением к ближайшему четному округляется если после запятой 5 и за ним нет никакой цифры

как округлить число 6,9?

Чтобы округлить число до целого, надо отбросить все числа, стоящие после запятой. Отбрасываем 9, поэтому предыдущее число следует увеличить на единицу. Значит, 6,9 приближенно равно семи целым.

На самом деле действительно не увеличивается цифра если после запятой 5 в любом финансовом учреждении

Гм. В таком случае финансовые учреждения в вопросах округления руководствуются не законами математики, а своими собственными соображениями.

Скажите, как округлить 46,466667. Запуталась

Если требуется округлить число до целого, то надо отбросить все цифры, стоящие после запятой. Первая из отброшенных цифр равна 4, поэтому предыдущую цифру не изменяем:

Уважаемая Светлана Ивановна. Плохо же Вы знакомы с правилами математики.

Правило. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т. е. последняя сохраняемая цифра оставляется неизменной, если она четная, и усиливается, если она нечетная.

И Соответственно: Округляя число 0,0465 до третьего десятичного знака, пишем 0,046. Усиления не делаем, так как последняя сохраняемая цифра 6 — четная. Число 0,046 столь же близко к данному, как 0,047.

Уважаемый гость! Да будет Вам известно, в математике для округление числа существуют различные способы округления. В школе изучают один из них, состоящий в отбрасывании младших разрядов числа. Я рада за Вас, что Вы знаете другой способ, но неплохо бы не забывать и школьные знания.

Спасибо вам большое! Нужно было округлить 349,92. Получается 350. Спасибо за правило

как правильно округлить 5499,8?

Если речь об округлении до целого, то отбросить все цифры, стоящие после запятой. Отброшенная цифра — 8, следовательно, предыдущую увеличиваем на единицу. Значит, 5499,8 приближенно равно 5500 целым.

Доброго дня! А вот такой вопрос возник сейас: Есть три числа: 60.56% 11.73% и 27.71% Каким образом окрулить до целых знаечний? Чтобы в сумме то 100 осталось. Если просто округлять, то 61+12+28=101 Плучается неувязочка. (Если, как тыт писали, по «банковскому» методу — в данном случае получится, но в случае, например 60.5% и 39.5% получится опять что-то пало — 1% потеряем). Как быть?

О! помог метод от «гость 02.07.2015 12:11″ Благодарю»

Не знаю меня в школе учили так: 1.5 => 1 1.6 => 2 1.51 => 2 1.51 => 1.6

Возможно, Вас так учили.

По моему у Вас ошибочка в последнем выражении. 1.5 => 1 1.6 => 2 1.51 => 2 «1.51 => 1.5»

0, 855 до сотых помогите пожалуйста

0, 855≈0,86 (отброшена 5, предыдущую цифру увеличиваем на 1).

Округлить 2,465 до целого числа

2,465≈2 (первая отброшенная цифра — 4. Поэтому предыдущую оставляем без изменения).

Как округлить 2,4456 до целого?

2,4456 ≈ 2 (так как первая отброшенная цифра 4, предыдущую цифру оставляем без изменения).

Исходя из правил кругления: 1,45=1,5=2, следовательно 1,45=2. 1,(4)5 = 2. Так ли это?

Нет. Если требуется округлить 1,45 до целого, отбрасываем первую цифру после запятой. Поскольку это 4, предыдущую цифру не изменяем. Таким образом, 1,45≈1.

А если мне нужно округлить 103, это будет 100 или 105? (нужно округлить до 0 или 5)

Ирина, 103 — это уже целое число. Округлять до целого его не нужно. Если требуется округлить 103 до десятков, тогда 103≈100.

Источник

Как округлить до трех значащих цифр в Excel

В Excel все решает пользователь. Программа округлит дробные или даже целые числа в зависимости какое число значащих цифр удовлетворит потребность пользователя. Несомненно, на первый взгляд такое округление может вызывать сомнение в рациональности решения. Однако в презентациях есть место быть как точным показателям, так и относительным. И в других ситуациях это также применимо. Например, в стратегическом планировании более важные относительные показатели, так как сколько не планируй никогда не угадаешь точные результирующие числа. В тактическом планировании более важны точные значения чтобы избежать серьезных просчетов. В стратегическом планировании где показатели достигают миллионов, каждое значение ниже определенного числа значащих цифр – не существенно.

Ниже на рисунке показано, как составить формулу, которая округляет миллионные числовые значения до заданного числа значащих цифр:

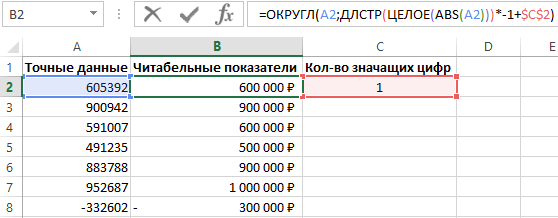
Функция ОКРУГЛ используется для округления исходного числового значения до определенного количества разрядов после запятой. Функция содержит 2 аргумента:

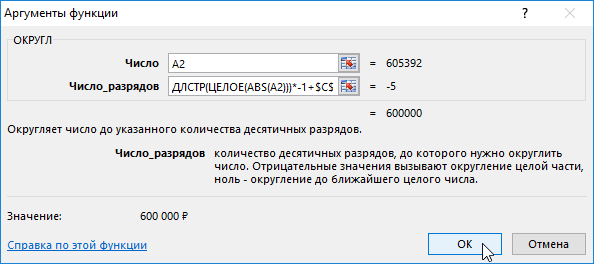
1. Число – ссылка на исходное значение, которое необходимо округлить.
2. Число-разрядов – количество разрядов, которое необходимо оставить после округления исходного числа.

Если во втором аргументе функции ОКРУГЛ указать отрицательное число, тогда Excel округлит исходное числовое значение в соответствии цифр по левой стороне запятой. Например, следующая формула возвращает в результате вычисления число 9500:

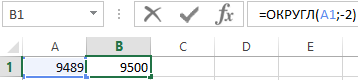
А если указать во втором аргументе значение -3, тогда функция ОКРУГЛ возвращает результат 9000:

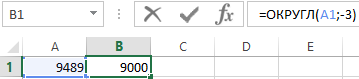
Такая формула прекрасно работает, но не всегда. Например, что будет если исходные числовые значения будут разных величин числовых радов? Одни будут более миллиона, другие едва превышают сотни тысяч. Если возникнет необходимость округлить все такие исходные значения до одной и той же значащей цифры используя при этом одну и туже формулу (как обычно принято в Excel). Применять для отдельных групп исходных значений функцию ОКГРУГЛ с разными значениями в аргументах – это не правильное, а точнее не наилучшее решение. Хотя теоретически все может сработать.

Для красивого решения данной задачи следует использовать постоянное неизменяемое число значащих цифр в формуле, которая вычислит соответствующие значения.

Правило встречается в следующих упражнениях:

5 класс

Задание 1270,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1274,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1276,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1277,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 853,
Мерзляк, Полонский, Якир, Учебник

Номер 855,
Мерзляк, Полонский, Якир, Учебник

Номер 856,
Мерзляк, Полонский, Якир, Учебник

Номер 857,
Мерзляк, Полонский, Якир, Учебник

Номер 858,
Мерзляк, Полонский, Якир, Учебник

Номер 1054,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 1,
Мерзляк, Полонский, Якир, Учебник

Номер 563,
Мерзляк, Полонский, Якир, Учебник

Номер 566,
Мерзляк, Полонский, Якир, Учебник

Номер 570,
Мерзляк, Полонский, Якир, Учебник

Номер 642,
Мерзляк, Полонский, Якир, Учебник

Номер 645,
Мерзляк, Полонский, Якир, Учебник

Номер 753,
Мерзляк, Полонский, Якир, Учебник

Номер 754,
Мерзляк, Полонский, Якир, Учебник

Номер 774,
Мерзляк, Полонский, Якир, Учебник

Задание 876,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник